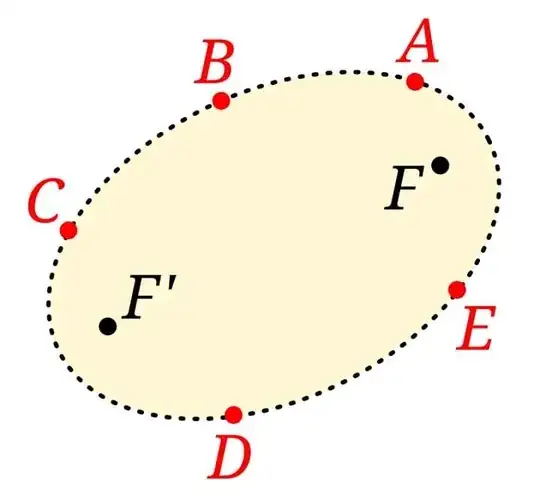
A conic section is uniquely defined by five distinct points on its circumference because two different conic sections cannot intersect at more than four points.
The elements of a conic section can be constructed with the knowledge of five of its points analytically, but this does not mean that it cannot be done geometrically, although the construction is difficult - and a challenge - but it can be done with the traditional tools of geometry, the ruler and the compass.
To solve the big problem, we will solve a series of step-by-step problems:
Create a sixth point at a random position.
This is done using Pascal's theorem
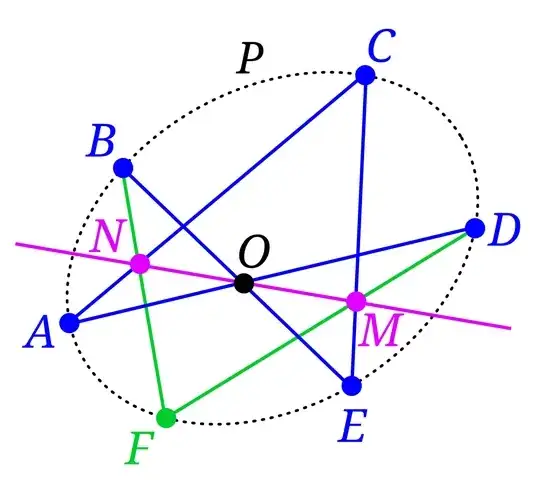
Constructing a chord passing through a known point and parallel to a known straight line.
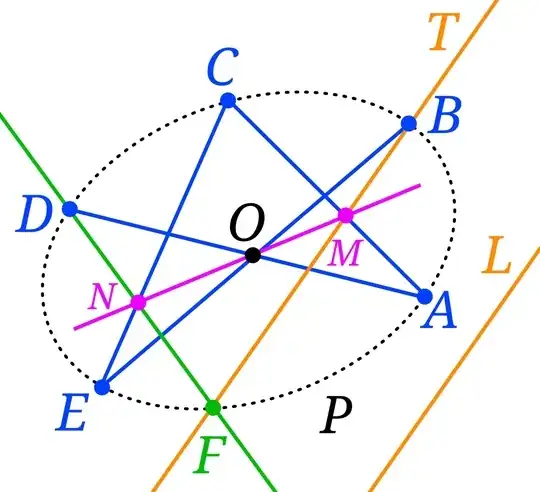
Create the center of the conical cut.
This is done based on the following theorem: The midpoints of parallel strings in a conic section pass through a center
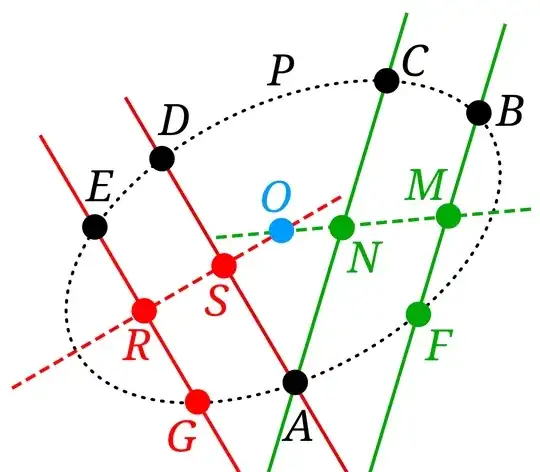
Create a tangent to a point.
Where the tangent is considered a special feature of the hypotenuse
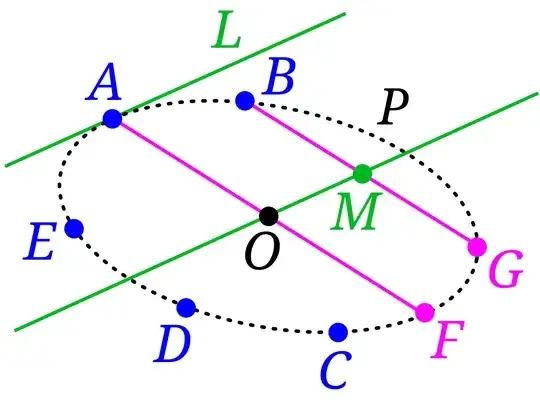Tangent can also be created using Pascal's theorem
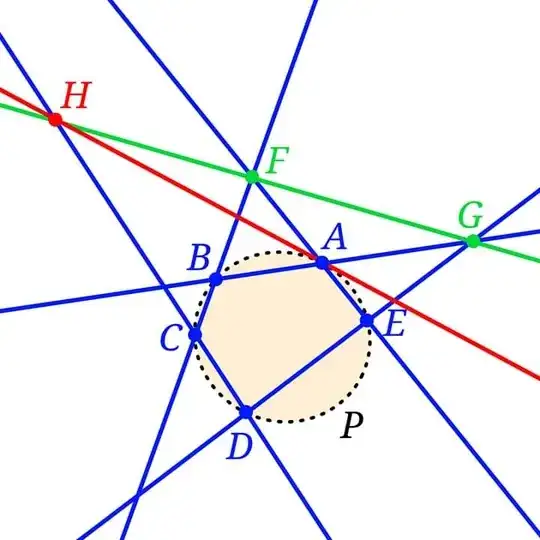
Create two conjugated chords.
This construct relies on the use of affine shunts
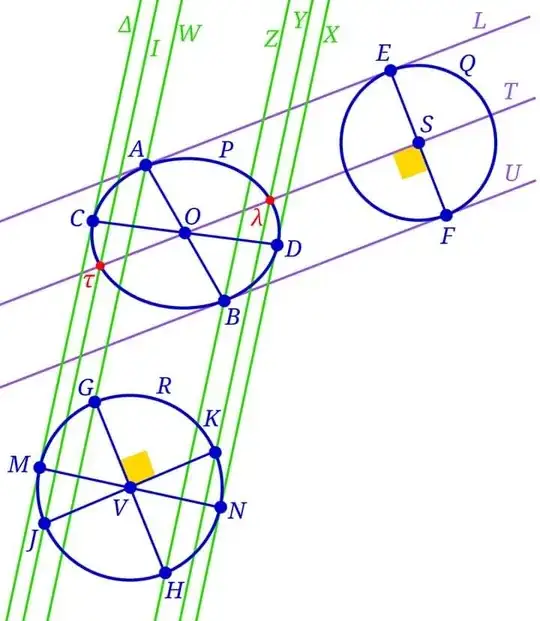
Determine the two axes of symmetry of the segments.
You can see the following link
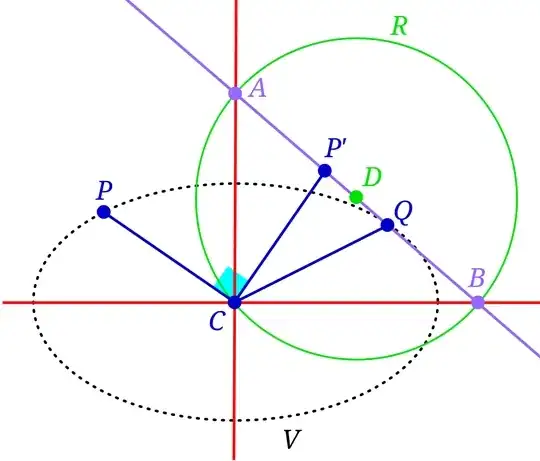7. Create two symmetrical tangents with respect to the axis of symmetry, then create the two foci.
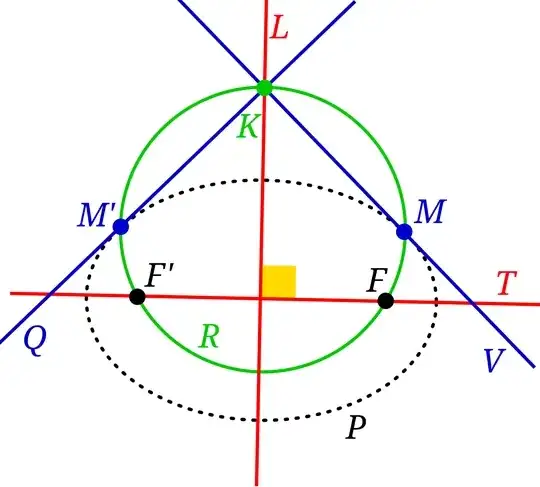
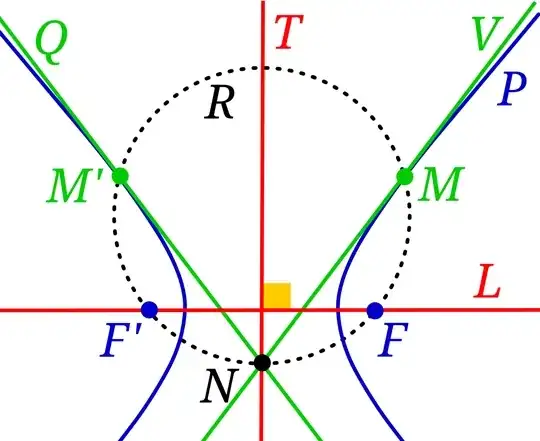
Finally, I apologize for the bad language as I write using Google Translate. Feel free to edit the text if you find this necessary
