What explains this peak probability "gain" in the birthday problem?

Question

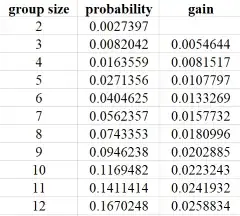
I was in class working out the probabilities in the birthday problem (assuming $365$ birthdates). As is commonly known, the probability that there is a birthday match among $n$ people is $$ B(n)=1 - \frac{P(365,n)}{365^n} = 1 - \frac{365!}{(365-n)!365^n}. $$ We generated a quick spreadsheet showing the group size $n$ and the probability of a match, just to gain an appreciation for how quickly the probability $B(n)$ approaches $1$.

To get insight into how the probability grows when you tack on one extra person, there was the suggestion to add a third column, which was the probability "gain" for lack of a better term: in the row for $n$ people we compute $$ B(n)-B(n-1). $$ So, a snapshot of the sheet looks like

Thus, for example, in going from $11$ to $12$ people we add about $2.59\%$ to the probability of match with $11$ people.

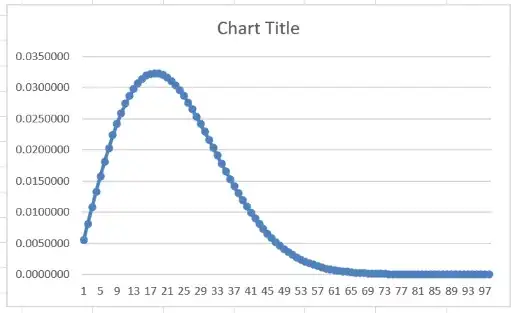
For fun, we worked this out for $1 \leq n \leq 100$ and there is interestingly (to me) a peak in the gain at $n=20$. This surprised me, thought I'm not sure why. I assumed the gain would decrease as the probability $B(n)$ gets closer to $1$, as there's less "headroom" to add much probability. This is true, but I incorrectly assumed some sort of monotonicity throughout.

What is the mathematical explanation for both the peak gain and its location? (Obviously this changes as you change the number of birthdates.) I've tried working out the difference $B(n)-B(n-1)$ but it's not insightful (to me). I can't do Calculus on this, as it's not continuous. Is this approximately some easily-seen continuous function, and that shows the maximum in a nice, intuitive way? How can we reason that a peak should occur at all?

Answer 1

Here's an intuitive calculation of where the peak gain should occur.

First of all, $B(n+1) - B(n)$ is the probability that $n+1$ people have a repeated birthday, but the first $n$ of them don't: so it's the probability that the $(n+1)^{\text{th}}$ person is the first to repeat a previous birthday.

So suppose that you are in a group of $365$ people lining up to write down their birthdays in a list, and the first person to write down a repeat birthday wins a prize. Thus far, $n$ people have written down their birthdays, and nobody's won yet. You're one of two people at the front of the crowd; should you go up, or should you nudge your neighbor to go up?

Well, if only one of you matches the list of $n$ birthdays so far, then it doesn't matter at all; no matter which of you goes first, the winner will be the same. However:

1. If both of you would be winners right now, then you would regret letting your neighbor go first. This has probability $\frac{n^2}{365^2}$.
2. If you and your neighbor share a birthday, then you want to let your neighbor go first. This has probability $\frac1{365}$.
3. Of course, if both 1 and 2 are true simultaneously, you still want to go first. This has probability $\frac{n}{365^2}$, which we should subtract from case 2.

So you want to go first when $\frac{n^2}{365^2} > \frac1{365} - \frac{n}{365^2}$, or $n^2 > 365 - n$, or $n^2 + n > 365$. This is false for $n \le 18$, but true for $n \ge 19$. Therefore, to maximize your chances of winning, you want to let $19$ people past you, and then jump in as the $20^{\text{th}}$ person.

In other words, the $20^{\text{th}}$ person stands the best chance of winning: the gap $B(20) - B(19)$ is the largest.

Answer 2

You can test for a maximum of the first difference of a discrete sequence by looking at the sign of the second order. A change of sign indicates the presence of a critical point. You can show that for the sequence $B_n=1-\frac{1}{K^n(K-n)!}$

$$\Delta^2B_n=B_{n+2}-2B_{n+1}+B_n=\frac{K-n(n+1)}{K^{n+2}(K-n)!}$$

A local maximum will be found at the position $n_0+1$ that satisfies $$K-n_0(n_0+1)>0~\wedge K-(n_0+1)(n_0+2)<0$$

It can be shown that $n_0=\lfloor\frac{\sqrt{4K+1}-1}{2}\rfloor$. For $K=365$, it requires the peak to be at $n=19$, which means the difference $B_{20}-B_{19}$ is the largest. In the edge case that $K=m(m+1), m\in\mathbb{N}$, it can be seen that $n_0=m, m+1$ are both maxima.

Answer 3

You want to do calculus, so for a continuous approximation, let $B_k(n)$ be the probability of a birthday collision among $n$ people in a $k$-day year (you've assumed $k = 365$).

The expected number of collisions is ${n \choose 2}/k \approx n^2/2k$. By the "Poisson heuristic" (the number of collisions is approximately Poisson-distributed) you have $B_k(n) \approx 1 - e^{-n^2/2k}$. You'd get the same thing out of Stirling's approximation.

Differentiating with respect to $n$ gives $$B^\prime_k(n) \approx {n \over k} e^{-n^2/2k}$$. As the product of a linear function and a decreasing exponential this will have a peak.

To figure out where the peak in $B_k^\prime(n)$ is, differentiate again to get

$$B_k^{\prime\prime}(n) = {k - n^2 \over k^2} e^{-n^2/2k}$$

and this will be zero when $k = n^2$, i. e. when $n = \sqrt{k}$. In your case, you have $\sqrt{365} \approx 19$.

Answer 4

Suppose you have a group of $n$ people chosen at random from a population with birthdays uniformly distributed over $365$ days of the year.

If $n$ is very small, so that the chance of a matching birthday is low, the probability that adding another random person to the group will match a birthday of someone already in the group is approximately $n/365.$

This probability clearly increases as $n$ increases. For small $n,$ where the expected number of distinct birthdays already in the group is very close to $n,$ the growth is almost linear with $n.$

Just to be clear, we're talking here about the probability that the $(n+1)$st person is the first one to match another person's birthday. That is, we're talking about the "gain" in your table. The "gain" from $B(n)$ to $B(n+1)$ is approximately $n/365$ for small $n.$

That's how I intuit the initial increase in gain. Obviously it can't increase forever because the infinite sequence of gains sums to $1,$ so there must be a maximum somewhere followed by a decrease to zero.

Answer 5

The probability $B(n)$ of at least one birthday match among $n$ people is (obviously) an increasing function of $n$. It is also bounded above, since a probability cannot exceed 1. Therefore the difference $D(n) = B(n) - B(n-1)$ must tend to zero as $n$ increases.

It's also intuitively obvious that, for small values of $n$, $D(n)$ is an increasing function of $n$: for each new person added to a group of $n-1$ people, the probability of that new person having a birthday match with someone already in the group is approximately equal to the expected number of such matches, which is simply $(n-1) \mathbin/ 365$.

So for small groups, where the probability of the group already having a birthday match before the $n$-th member is added is still much less than one, $D(n)$ increases approximately linearly with the size of the group.

---

Those two observations are all that's needed to explain the general shape of the curve you plotted.

Basically, for any function $f(n)$ with the following properties:

1. $f(n)$ is a monotone increasing function of $n$;
2. $f(n)$ is bounded above; and
3. for small $n$, $f(n) - f(n-1)$ is approximately proportional to $n$;

the plot of $f(n) - f(n-1)$ will look something like your graph: an initial linearly increasing part (due to property 3) followed by a decrease towards zero (due to properties 1 and 2), with a peak in between (because a graph that initially increases and then decreases must necessarily have a maximum between the increasing and the decreasing portion).

(Of course there could be multiple peaks, if the growth of $f(n)$ temporarily flattens out and then starts increasing again. But there has to be at least one.)