4

From this question we have the following.

If $n$ persons are randomly allocated to $q$ rooms, then the probability of having exactly $m$ rooms with each exactly $k$ persons is given by

$$ \large p(n,q,m,k) := \frac{1}{q^n}\sum_{j=m}^{\min(q, \left\lfloor \frac{n}{k} \right\rfloor)} (-1)^{j-m} \binom{j}{m} \binom{q}{j} \binom{n}{jk} \frac{(jk)!}{(k!)^j}(q-j)^{n-jk}. $$

My question is:

For given $q,m,k$ what is the $n$ that maximizes $p$?

In another words: how many people should we put in the $q$ rooms to maximize the probability that there are exactly $m$ rooms containing exactly $k$ persons?

(Possibly another question: what if we're also allowed to vary $q$.)

My try: If we let $X$ be the number of rooms with exactly $k$ persons, then (using indicator random variables and linearity)

$$ \mathbb{E}[X] = q \binom{n}{k} (q-1)^{n-k} q^{-n} $$

and in order to maximize $\mathbb{P}(X=m)$, heuristically we should have $\mathbb{E}[X] \approx m$. If we approximate $\binom{n}{k}$ by $\frac{1}{k!} n^k$, we get the equation

$$ n^k \left(1-\frac{1}{q}\right)^n = \frac{k! m(q-1)^k}{q} $$

to which Wolfram Alpha gives a solution in terms of the Lambert-W function

$$ n = \frac{k}{\log(1-1/q)} W\left( \frac{1}{k} \log(1-1/q) \left( \frac{k!m}{q} \right)^{1/k} \right) \tag{1}. $$

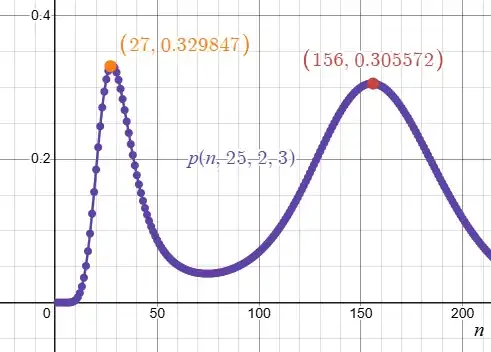
For large $q$ this seems to agree with numerical experiments. The function $n \mapsto p(n,q,m,k)$ appears to have two peaks. The first one approximately given by (1) and the second one (it seems) if we use $W_{-1}$, another branch of the Lambert-W function. But it also looks like the first one is always bigger.

example with q=27, m=2, k=3

ploosu2
  • 12,367
  • I am not sure that I understand your chart. With $27$ rooms and $122$ people, my simulations suggest the probability of exactly $3$ rooms with exactly $4$ people each is just over $0.12$, while with $27$ rooms and $17$ people the probability of exactly $3$ rooms with $4$ people each is less than $0.0001$. It suggests you might do better with about $60$ people giving a probability of about $0.26$, not a surprise since with $60$ people the expected number of rooms with exactly $4$ people in is $27 {60 \choose 4}\left(\frac1{27}\right)^{4}\left(1-\frac1{27}\right)^{60-4} \approx 2.9932$. – Henry Mar 26 '25 at 17:01
  • @Henry Oops, I had wrong $m$ and $k$ in that picture. Also I had the order of them reversed in Desmos. Now it should be correct. Thanks for pointing it out. – ploosu2 Mar 26 '25 at 18:04
  • Your edited chart now makes more sense to me. There are a couple of issues with your approximation: (a) getting the mean almost exact may not give precisely the maximum likelihood point though it should be reasonably close and (b) the $n^k$ may be slightly too large when trying to find the mean point, and something like $\left(n-\frac{k-1}2\right)^k$ may sometimes be better. But as an approximation it seems to work reasonably well. – Henry Mar 27 '25 at 00:20
  • The reason for two peaks may be that for intermediate values of $n$ you tend to get too many rooms with $k$ people, while with values of $n$ outside the peaks you may tend to get too few rooms with $k$ people (typically more rooms with fewer than $k$ people below the first peak and more rooms with more than $k$ people above the second peak). The first peak may be higher than the second because with fewer people there would fewer possibilities, making each possibility have a higher probability. – Henry Mar 27 '25 at 00:40
  • I also suspect that there might be other examples with large enough $m$ for given $q$ and $k$ where there is a single peak and there is never a suitable mean hitting value so your approximation might not work. Try for example $q=25, m=10, k=3$. – Henry Mar 27 '25 at 00:45

0 Answers0