Minimal graph of given genus (number of handles that must be added to the plane to embed the graph without any crossings) for 3+

Question

The genus $\gamma(g)$ of a graph $g$ is the minimal integer $n$ such that the graph can be embedded in a surface of genus $n$ without any crossings.

Let's focus on connected, simple graphs (no loops, no multi-edges).

What is the minimal graph of genus $n$?

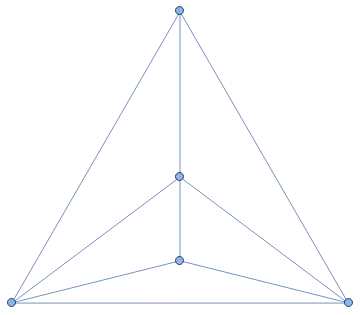
For $n=0$, the singleton graph, just a vertex, no edges should do.

For $n=1$, the smallest 'toroidal graph' is the 'pentatope' or $K_5$ graph, the complete graph with $5$ vertices and $10$ edges. For a 'graphical proof' see Is the following embedding of $k5$ on torus not a 2-cell embedding? If not, how can we get the 2-cell embedding of $k5$ on the torus?.

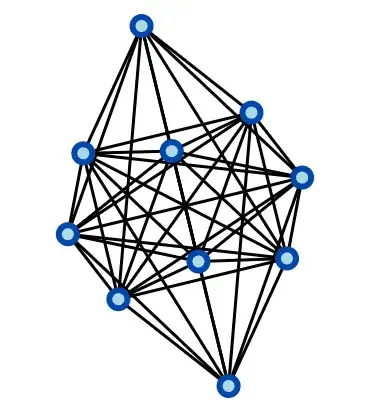
For $n=2$, there is a 'double-toroidal' graph with $8$ vertices and $22$ edges

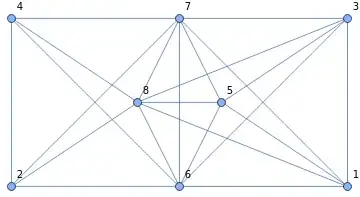
In Mathematica, it is g=GraphData[{"DoubleToroidal",{8,2}}]... and seems to be missing in the house of graphs.

The respective graph complement is the 3-dipyramidal graph GraphData[{"Dipyramid",3}] (plus 3 singletons/ single vertices) which can also be found at https://houseofgraphs.org/graphs/450

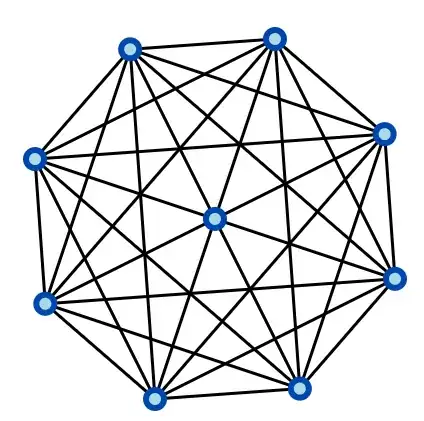
For $n=3$, there is a 'pretzel' graph with $9$ vertices, e.g., $K_9$ with $36$ edges but the house of graph lists a genus 3 graph with $32$ vertices: https://houseofgraphs.org/graphs/394

... that can be imported to Mathematica and displayed with Graph[CanonicalGraph[ImportString["H~z\z~~", "Graph6"]], GraphLayout->"CircularEmbedding",VertexLabels->Automatic]

This graph can be constructed from the complete graph with $9$ vertices by removing $4$ unlinked, single edges (put differently, the graph complement consists of a singleton/ single vertex and $4$ $P_2$ graphs).

I have not seen any claim in that direction, so,

Is this graph the minimal genus 3 graph?

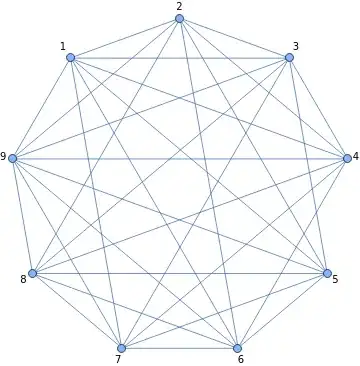
For $n=4$, there is a 'genus n' graph with $10$ vertices, e.g., $K_{10}$ with $45$ edges but the house of graph lists a genus 4 graph with $44$ vertices: https://houseofgraphs.org/graphs/150

This must be the graph constructed from the complete graph by removing one edge (here $1-2$)

Is this graph the minimal genus 4 graph?

References

• https://en.wikipedia.org/wiki/Planar_graph
• https://en.wikipedia.org/wiki/Graph_embedding
• https://en.wikipedia.org/wiki/Toroidal_graph
• https://en.wikipedia.org/wiki/Genus_(mathematics)
• https://mathworld.wolfram.com/Double-ToroidalGraph.html
• https://mathworld.wolfram.com/PretzelGraph.html
• https://mathworld.wolfram.com/GraphGenus.html
• Is there a minimum number of vertices that a graph must have to be of a given genus?
• Genus of a graph and planarity
• Genus of a graph
• Why can the complete graph K5 be embedded on a torus?
• can graph $K_5$ be embedded in a Möbius band?

---

Not quite sure:

• It seems that one issue is the lack of a simple and effective way to calculate the genus of a graph and test more graphs
• The other issue is that there is no 'simple' proof to show a genus n graph (derived by edge deletion from the complete graph) is minimal

Views?