Genus of a graph and planarity

Question

In 'Introduction to graph theory' by Trudeau it is proved the theorem

Every graph has a genus

by first embedding the graph onto a sphere , and then adding handles, say we use $k$ of them, where the graph has edge-crossing , this is the example used :

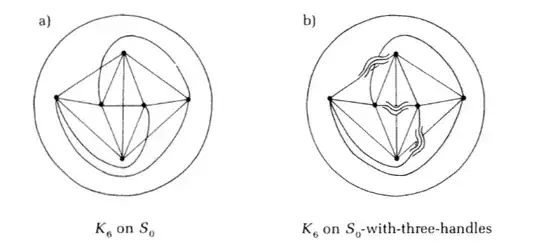
Then, he writes that using a continuous deformation of the surface (stretching,shrinking or distorting the surface) it is possible to preserve planarity while deforming the $k$-handles sphere into a $k$-hole torus. So, the genus will be at most $k$.

I'm not able to visualize the bold part, how can I be sure that planarity will be preserved? Should it be obvious? Is there a simple explanation to understand clearly why this happens ? (I'm totally a beginner in algebraic topology, just visualization of trasformations are used in the book).

Another proof of a theorem stated earlier in the book : "every planar graph has genus $0$ (it can be embedded on a sphere)" was obscure to me but then searching online I found the explanation through the stereographic projection and all my doubts were gone , does something similar exist? Or even a good intuition is difficult to set up ?

EDIT :

For clarity I add the definition of genus given in the book :

The genus of a graph, denoted $g$, is the subscript of the first surface among the family $S_0,S_1,S_2,\dots$ on which the graph can be drawn without edge crossing .

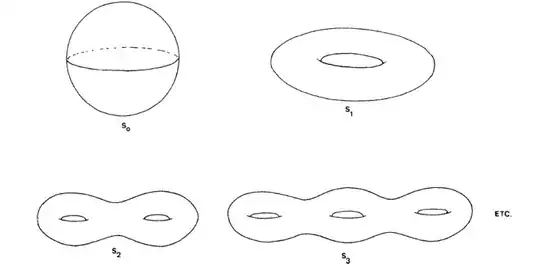
I also add the explanation of the author to pass from the $k$-handle sphere to the $k$-hole thorus :

Think of the surface consisting of $S_0$ with $k$ handles as made of extremely pliable rubber which we are free to stretch, shrink or otherwise distort as much as we want , provided that we don't tear it off of fold it back onto itself. With this understanding we see that the surface consisting of $S_0$ with $k$ handles can be 'continuously deformed' into $S_k$ and the vertices and edges of $G$ can be carried along with this continuos deformation. Thus $G$ can be drawn on $S_n$ without edge-crossings.

The bold part is obscure to me in the sense explained above.

Answer 1

To be honest, I am not really sure what is your question. What do you mean by "every graph has a genus"? I'll try to answer by the way, since geometrically your question is clear.

For me, the genus is a well defined quantity associated to a (compact) surface. When you have a planar graph, you imagine to fill the faces among the edges and you get a very simple surface, something like a polygon in the plane. If you also fill the exterior " ghost" face you obtain the whole plane. The genus is computed now as $1-\chi/2$, where

$$\chi = \#\{\text{filled faces}\} - \#\{\text{edges}\} +\#\{\text{vertices}\}$$

And we would be done, but the plane is not a compact surface so we don't know what this should be equal to. To deal with this technical issue, we add a point to infinity and we get a sphere. Now the theory tells us that the genus (which is secretly the number of holes) of the sphere is zero, so that we get for a planar graph

$$\#\{\text{filled faces}\} - \#\{\text{edges}\} +\{\text{vertices}\}= 2$$

You can also reformulate this, recalling that the faces we filled were the internal faces + one ghost face: $$\#\{\text{ faces}\} = \#\{\text{edges}\} - \{\text{vertices}\}+1$$

Check this on small graphs! That's true for real :)

Some complications arise if there are intersections. The main idea in algebraic topology is that if we cut a topological space in simple bricks - like a surface in triangles - the geometric properties of the space become combinatorial properties of how our bricks are combined. You have just seen this above: the genus of the sphere reflects in an equation for edges, vertices and faces for the graph that "builds up" the sphere.

When you have intersection, the problem is that the graph is apparently not building up anything. The idea of your book is to create small bridges (handles) so that the graph does not intersect himself anymore: you will have a planar graph sitting inside a new surface, no longer a sphere, but who cares! We can carry on our argument above, and we only have to change the genus in the end: for a nice coincidence, it will be the number of bridges we added.

If you are not comfortable with deforming the surface into a k-hole torus while preserving planarity, there is no need to do that: the genus is a homotopy invariant. If you are convinced that - beside the graph story - you can deform a k-handle sphere into a k-hole torus, then you know that the genus of the k handle sphere is the same of the k-hole torus, that is k.

Please ask in the comments if you need further clarifications :)

Answer 2

If you have a mug (that has glaze on it) and a whiteboard marker, try drawing $K_5$ on it without any edge crossings.

Once you do that, it's not a far leap to imagine the handle expanding to make the mug more donut-like, and noticing that this deformation does not create any new edge crossings. Then try generalizing this to more holes.

Answer 3

Maybe I found a satisfactory not much mathematical way for myself to explain what's going on.

Take a nonplanar graph on a sphere with $1$ unavoidable intersection, then you can add a bridge to delete the intersection, so now if we are able to imagine the trasformation in a torus we are done in the case of one intersection. Take the bridge and make it say an half ring, this is simple enough for me to see that it preserves planarity, now we will have something like a kettlebell, now get bigger the half ring so that it incorporates the sphere, here we have the torus!

Now, say we have a graph with $k$ unavoidable intersections , then we can add $k$ bridges one by one (applying the trasformation above each time) so at most the genus is $k$.