Shape formed by repeatedly replacing set of points with midpoints

Question

This is a partial follow-up to this question.

---

Suppose we start off with a (finite) set of points $S_0\subset \mathbb{R}^2$. Repeat the iteration $$S_{k+1}=\left\{\frac{p+q}{2}\mid p,q\in S_k\wedge p\not=q\right\}$$ which is getting the set of midpoints between all pairs of points. It looks like there is always an open set $T\subset \mathbb{R}^2$ that $S_k$ 'approaches'. By this, I mean that it looks like for all $\epsilon>0$, there is some $K$ such that for all $k\ge K$, $0<\max_{p\in S_k}d(p,T)<\epsilon$.

If $|S_0|\le 2$, then $T$ is the empty set. If $|S_0|=3$, it would converge to a point, which also corresponds to the empty set (since we have the stipulation that $T$ is open). But it already gets complicated when $|S_0|=4$, even when it's a square (arguably the simplest example with $4$ points). Moreover, if we say $S_0$ is any arbitrary (finite) set of points in $\mathbb{R}^2$, the number of elements in $S_k$ blows up super-exponentially. With $|S_0|=4$, the number of elements in $S_k$ is about $2\cdot c^{2^n}$, where $c\approx 1.28$. However, if we restrict $S_0$ to only be points lying on some lattice, the number of points "only" increases exponentially.

I think the case of a square is the smallest interesting example - what is $T$ if we start off with a square?

Let's say $S_{-2}=\{(-2,-2),(-2,2),(2,-2),(2,2)\}$, the square with side lengths $4$, so that $S_0=\{-1,0,1\}^2$. I had a side length of $4$ at the beginning because the radius of the smallest circle containing $S_k$ approaches $1$.

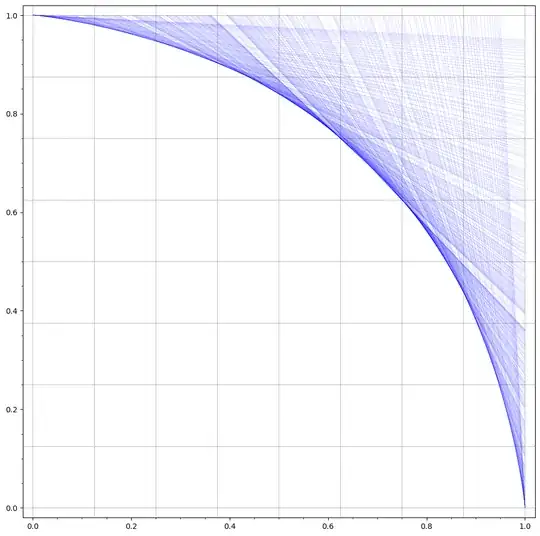
Define the safe points $S_k'\subseteq S_k$ to be those that will always remain in future iterations. These are precisely the points $p\in S_k$ such that there exist two different $x,y\in S_k$ such that $x+y=2p$. Let $A_k$ be the convex hull of $S_k'$, and $B_k$ be the convex hull of $S_k$. Then $A_k\subseteq S_{k+1},T\subseteq B_k$, so we can keep refining what $T$ is. It also looks like $B_k\setminus A_k$ has area approaching $0$ (which implies that we can define $T$ as the 'limit' of $A_k$ or of $B_k$).

Numerically, it looks like the slope of the boundary of both $A_k$ and $B_k$ is $-1$ from $5/8$ to $3/4$. It's possible that we can figure out the slope of the boundary for an arbitrary $x\in(0,1)$, and then use that to identify the boundary of $T$, but I'm not sure how to analytically find the slope or even if it's well-defined. It probably isn't well-defined for much of the set $\left\{\frac{a}{2^b}\mid a,b\in\mathbb{Z}\right\}$, since the convex hulls could have cusps at those points.

Based on $S_{18}$, the area of $A_{18}$ is $\frac{51901287739}{4^{17}}=3.0210525\dots$, while the area of $B_{18}$ is $\frac{51901289787}{4^{17}}=3.0210526\dots$. This implies that the area of $T$ (assuming the area of $B_k\setminus A_k$ goes to $0$) is $3.021052\dots$.

My questions are about the area of $T$ and the shape of the boundary of $T$. How can we find either/both of these?

This picture shows what the top-right part of $S_8$ looks like. The black indicates the actual points in $S_8$, while the red is the part of the radius-$1$ circle that is not in $S_8$.

Answer 1

The only thing im thinking about is that the infinite set $M:=\{\frac{a}{2^b} | a, b \in \mathbb{Z}\}$ is a midpoint-convex set but not convex set iirc. So under your construction of $S_k$, with $S_0:=M$ would be a constant Sequence. Also I think other definitions of convergence might be useful. Maybe something like looking at the convex hull of $C(S_k)$ and saying something like that the area of $C(S_k)\setminus C(S_{k+1})$ goes to zero, then $(S_k)$ is in some sense cauchy/convergent? im not sure.

The $0< \max \dots$ in your definition makes me worry, cuz i imagine there are some $(S_k) $ where we want convergence where after some Iterations the set stays constant as a (midpoint)-convex set, where we would need $0 \leq$. However if we do that, then any arbitrary big enough convex set does the job for a given $S_k$ so we would only be interested in the smallest convex set with the convergence property.

Answer 2

This answer, far from being a formal proof, is a collection of empirical observations.

I changed the code in Qiaochu Yuan's answer to delete interior points at each step and I ran $16$ steps of the process (which should be $S:=S_{14}$; it seems that your code has better optimizations, as you have a representation of $S_{18}$). Then, using SageMath, I found the convex hull $B:=B_{14}$.

If an edge $e$ in $\partial B$ contains $k\ge 3$ points $s_1, s_2, \dots, s_k$ of $S$, then $\partial T$ contains the segment $s_2s_{k-1}$ (which degenerates to a point if $k = 3$); indeed, the line $s_1s_k$ intersects $\partial T$ exactly in that segment (or point).

By looking at the edges of $B$ and discarding those which do not have enough points of $S$, I found various patterns in the supporting lines. For simplicity, we look at the region $x\ge y \ge 0$. Let $n \ge 1$ and let $0 \le r < n$ be coprime with $n$. Then, for each $k\ge 1$, there is a supporting line of slope $$ \sigma := -\frac{nk + r}{n} < 0 $$ with equation $$ ny + (nk+r)x = nk+r + 2^{-k}q(n,r), $$ where $q(n,r)$ is independent of $k$. Indeed, for $0 < r \le n/2$, let $s := n \bmod r$. Then we have:

\begin{align} q(1,0) &= \frac{3}{4}, \\[2ex] q(n,r) &= \frac{1}{16}(\alpha(r, s)\cdot 2^{-\lfloor n/r\rfloor} + 12n-8r), \\[2ex] q(n,n-r) &= \frac{1}{16}(\alpha(r, s)\cdot 2^{-\lfloor n/r\rfloor} + 6n+4r), \end{align}

where $$ \alpha(r, s) = \begin{cases} 3 & \text{if $r=1$,} \\ 3r+3\cdot 2^{-r-2}-\frac{3s+1}{2} & \text{otherwise.} \end{cases} $$

It also appears that the supporting lines intersect $\partial T$ in segments of positive length in three cases:

• the slope is $\sigma = -1$;
• $n = 2$ (and $r = 1$);
• $n \ge 5$ and $r\in \{2,n-2\}$.

This should give a complete parametrization of the polar dual of $T$. Of course, I have no idea how to prove these formulas, or if they are correct for large values of $n$; the mere implication that the supporting line varies continuously as a function of $\sigma$ is daunting to say the least. In any case, the patterns seem to hold very strongly in all the cases I examined.

---

EDIT: Here's a plot of $T$ (in the first quadrant) obtained as an envelope of the lines defined by the formulas above. I used rational numbers with numerators and denominators not exceeding $20$. The grid spacing is $1/8$; note the straight segment $(5/8, 6/8) - (6/8, 5/8)$.

---

EDIT: I considered the polygon $T(n)$ bounded by lines whose slopes have $\text{numerator} + \text{denominator} \le n+1$. Clearly $T = \bigcap_{n\ge 0} T(n)$. It appears that $$ \mathrm{Area}(T(n)) = 3.0210537\ldots + O(n^{-1}e^{-\sqrt{n}}), $$ which contrasts with your estimate $\mathrm{Area}(T) = 3.021052\ldots$. If your calculation is correct, this may indicate that my formulas do not hold for $n$ large.