Span of the vertices of a regular tetrahedron

Question

I'm curious about representations of certain abelian groups in $\Bbb{R}^n$, whether they are lattice or dense.
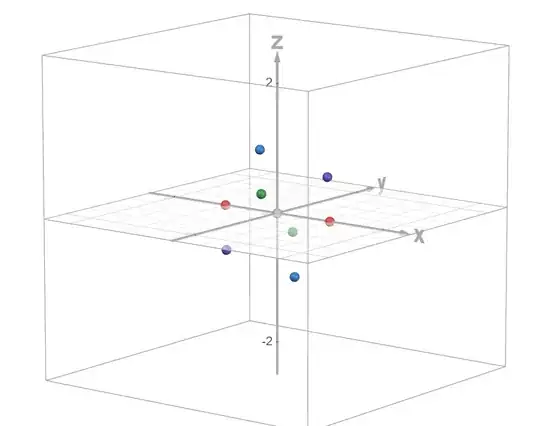
In particular, I was interested in the following group on four generators: $$G := \{ r, b, g, p: r+b+g+p = 0 \}$$ I selected the following four vectors (color coded $r$ = red, $b$ = blue, $g$ = green, $p$ = purple) to represent this group in $\Bbb{R}^3$. For symmetry's sake, I let them be the four vertices of a regular tetrahedron: 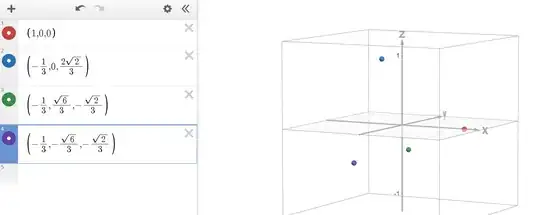Letting $\vec{x}$ represent the vector representation of generator $x$, we have \begin{align*} \vec{r} &= ⟨1, 0, 0⟩ \\ \vec{b} &= ⟨-1/3, 0, 2\sqrt{2}/3⟩ \\ \vec{g} &= ⟨-1/3, \sqrt{6}/3, -\sqrt{2}/3⟩ \\ \vec{p} &= ⟨-1/3, -\sqrt{6}/3, -\sqrt{2}/3⟩ \ \end{align*}

Originally I thought the span of these four vectors under addition would be dense in $\Bbb{R}^3$, but after some cogitation, I now believe the span would be a body-centered cubic lattice, just with a weird orientation in space.
Can anyone either confirm or deny that this is the case?
Also, how would I rotate the "canonical" BCC lattice (with vertices at the integer points and half-integer points of $\Bbb{R}^3$) to get the version that we have here? In addition to stretching everything by $2\sqrt{3}/3$, I mean.

Edit: I added the negatives of each of the four vectors above (negative has the same color as the original), together with the origin (gray), to visually clarify the potential BCC nature of the lattice.

Answer 1

This is a regular tetrahedron so the vertices add up to $0$, which is why they're a representation of $G$. That means you get the lattice spanned by any $3$ of them. It's related to the tetrahedral-octahedral honeycomb so it looks like $A_3$, or the face-centered cubic. I think you get that from thinking of $A_3$ in its incarnation as $$A_3 = \{ (x_1, x_2, x_3, x_4) \in \mathbb{Z}^4 : x_1 + x_2 + x_3 + x_4 = 0 \}$$

(which is of course a version of $G$), then suitably orthogonally projecting this lattice to $\mathbb{R}^3$ and scaling.

Edit: Okay, I found a picture that makes it clearer in this math.SE answer by J.M.; there's a tetrahedron inside a cube:

                                         

Taking the center of this cube to be the origin and the vertices to be $(\pm 1, \pm 1, \pm 1)$, this gives that there's a regular tetrahedron centered at the origin with vertices

$$(1, 1, 1), (-1, -1, 1), (1, -1, -1), (-1, 1, -1)$$

whose span is the sublattice

$$A_3 \cong \{ (x_1, x_2, x_3) \in \mathbb{Z}^3 : x_1 + x_2 + x_3 \equiv 0 \bmod 2 \}$$

of $\mathbb{Z}^3$ consisting of lattice points whose coordinate have even sum; this is a copy of $A_3$. It contains cubes of side length double the cubes pictured above, and the midpoints of their faces, so there's the face-centered cubic also.

Answer 2

Also, how would I rotate the "canonical" BCC lattice (with vertices at the integer points and half-integer points of $\Bbb{R}^3$) to get the version that we have here? In addition to stretching everything by $2\sqrt{3}/3$, I mean.

I'm assuming the canonical BCC lattice points are

$p=(-1, -1, -1),g= (1,1,-1),b=(-1,1,1),r= (1, -1, 1)$

You have to multiply 2 rotation matrices

$$ \frac{1}{\sqrt 3} \begin{bmatrix} \sqrt{\frac{2}{3}} & 0 & \frac{1}{\sqrt3} \\ 0 & 1 & 0 \\ -\frac{1}{\sqrt3} & 0 & \sqrt{\frac{2}{3}} \end{bmatrix} \begin{bmatrix} \frac{1}{\sqrt2} & -\frac{1}{\sqrt2} & 0 \\ \frac{1}{\sqrt2} & \frac{1}{\sqrt2} & 0 \\ 0 & 0 & 1 \end{bmatrix} = $$ $$ \frac{1}{\sqrt 3} \begin{bmatrix} \frac{1}{\sqrt{3}} & -\frac{1}{\sqrt{3}} & \frac{1}{\sqrt{3}} \\ \frac{1}{\sqrt{2}} & \frac{1}{\sqrt{2}} & 0 \\ -\frac{1}{\sqrt{6}} & \frac{1}{\sqrt{6}} & \sqrt{\frac{2}{3}} \end{bmatrix} $$

For example if you right multiply the matrix by $r= (1, -1, 1)$ you get $r'= (1, 0, 0)$.

The first matrix rotates by the $z$ axis, then by the $y$ axis.