Roots of $\tan^{-1}\frac{2x}{1-x^2}+\cot^{-1} \frac{1-x^2}{2x}=\frac{\pi}{3}$ (IIT-JEE)

Question

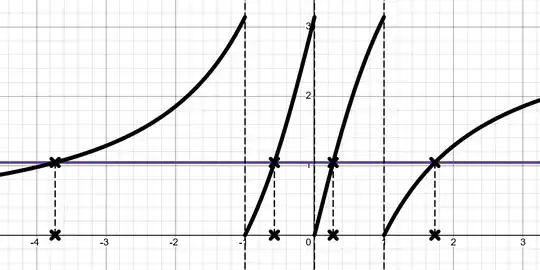
For the equation (IITJEE-M-Jan-2023) $$\tan^{-1}\frac{2x}{1-x^2}+\cot^{-1} \frac{1-x^2}{2x}=\frac{\pi}{3},\tag{1}$$ usually, two roots: $-1/\sqrt{3}$ and $2-\sqrt{3}$ belonging to $[-1,1]$ are found and discussed. We show two more roots here.

Case$(1)$ $x<-1$: Both the arguments in $(1)$ are positive so we can re-write it as $$2\tan^{-1}\frac{2x}{1-x^2}=\frac{\pi}{3}\implies x^2+2\sqrt{3}x-1=0 $$ giving us two root $x=-2\pm \sqrt{3}$, here we choose $x=-2-\sqrt{3}.$

Case (2) $x>1$: We can re-write $(1)$ as $$\tan^{-1} \frac{2x}{1-x^2}+\pi+\tan^{-1}\frac{2x}{1-x^2}=\frac{\pi}{3}$$ $$\implies 4 \tan^{-1} x-2\pi+\pi=\frac{\pi}{3}\implies \tan^{-1}x=\frac{\pi}{3}.$$

So we get $x=\sqrt{3}$.

The question is whether Eq. $(1)$ has other root(s)?

Edit Also see Why $\cot^{-1}x$ is an odd function in Mathematica

Answer 1

No, and it is easy to see why. Define $$ f(x) = \tan^{-1}\frac{2x}{1-x^2}+\cot^{-1} \frac{1-x^2}{2x} $$ Then with some algebra one sees $$ f'(x) = \frac{2 (3 + x^4)}{(x^2 + 1) \left( \left(x^2 - \frac 3 2 \right)^2 + \frac 7 4 \right)} $$ Note that the denominator is strictly positive, so $f' > 0$ and hence $f$ is increasing wherever $f$ is defined. The only such problematic points are $x \in \{0,-1,+1\}$, clearly (they cause divisions by zero).

So, on each interval $(-\infty,-1)$, $(-1,0)$, $(0,1)$, and $(1,\infty)$, $f$ may have at most one root. With the collection of all four roots known, then, no other real roots can exist.

(Desmos link.)

Answer 2

Let us copy the equation :

$$\tan^{-1}\left(\frac{2x}{1-x^2}\right)+\cot^{-1} \left(\frac{1-x^2}{2x}\right) =\frac{\pi}{3}\ \tag{E}$$

You have found $3$ out of $4$ solutions. You have missed solution $x=\tfrac13 \sqrt{3}$.

Here is why.

Let us start from the fact that :

$$\cot^{-1}(u)=\begin{cases}\tan^{-1}(\tfrac1u)+\pi& \text{if} \ u>0\\ \tan^{-1}(\tfrac1u)& \text{if} \ u<0 \end{cases}$$

(it can be taken as a definition of $\cot^{-1}(u)$)

With this definition, we can transform $(E)$ according to two cases :

• First case : if $u:=\tfrac{2x}{1-x^2} > 0$, $(E)$ becomes :

$$2 \tan^{-1}(\tfrac{2x}{1-x^2})+\pi=\tfrac{\pi}{3}$$

which is equivalent to :

$$\tfrac{2x}{1-x^2}=\underbrace{\tan(-\tfrac{\pi}{3})}_{-\sqrt{3}}$$

giving a quadratic equation whose roots are

$$x_1=-\sqrt{3}, \ \ \ x_2=\tfrac13 \sqrt{3}$$

• Second case : if $u:=\tfrac{2x}{1-x^2} < 0$, $(E)$ becomes :

$$2\tan^{-1}(\tfrac{2x}{1-x^2})=\tfrac{\pi}{3}$$

which is equivalent to :

$$\tfrac{2x}{1-x^2}=\underbrace{\tan(\tfrac{\pi}{6})}_{\tfrac13\sqrt{3}}$$

giving a quadratic equation whose roots are

$$x_3=-2-\sqrt{3}, \ \ \ x_4=2-\sqrt{3}$$

Remark : please note that we find the same roots as @PrincessEev.

Answer 3

Slightly deviating from @JeanMarie,

Using What is $\arctan(x) + \arctan(y)$,

$$2\tan^{-1} x = \begin{cases}\tan^{-1}\left(\dfrac{2x}{1-x^2}\right), &x^2 < 1\iff-1<x<1 \\[1.5ex] \pi + \tan^{-1}\left(\dfrac{2x}{1-x^2}\right), &x>0,x^2>1\iff x>1 \\[1.5ex] -\pi + \tan^{-1}\left(\dfrac{2x}{1-x^2}\right), &x<0,x^2>1\iff x<-1\end{cases}$$

Using Are $\mathrm{arccot}(x)$ and $\arctan(1/x)$ the same function?,

$$\text{arccot}y=\begin{cases}\tan^{-1}\dfrac1y, &y>0 \\[1.5ex] \pi + \tan^{-1}\dfrac1y, &y<0\end{cases} \implies\tan^{-1}\dfrac{2x}{1-x^2}=\begin{cases}\dfrac\pi6, \text{ if }\dfrac{2x}{1-x^2}>0 \\[1.5ex] \dfrac{-\pi+\dfrac\pi3}2=-\dfrac\pi3, \text{otherwise}\end{cases}$$

Now let us verify the signs of $x(x-1)(x+1)$

Case $\#1:x<-1, \dfrac{2x}{1-x^2}>0$

Consequently, $2\tan^{-1} x =-\pi + \tan^{-1}\left(\dfrac{2x}{1-x^2}\right)=-\pi+\dfrac\pi6,x=\tan\left(-\dfrac{5\pi}{12}\right)=\cdots=-\cot\left(\dfrac\pi2-\dfrac{5\pi}{12}\right)=-\dfrac{1+\cos\dfrac\pi6}{\sin\dfrac\pi6}=?$

Case $\#2:-1<x<0,\dfrac{2x}{1-x^2}<0$

Case $\#3:0<x<1,\dfrac{2x}{1-x^2}>0$

Case $\#4:x>1,\dfrac{2x}{1-x^2}<0$

Using $\tan A=\dfrac{1-\cos2A}{\sin2A},\cot B=\dfrac{1+\cos2B}{\sin2B}$