Why $\cot^{-1}x$ is an odd function in Mathematica

Question

The function $f(x)=\cot^{-1} x$ is well known to be neither even nor odd because $\cot^{-1}(-x)=\pi-\cot^{-1} x$. it's domain is $(-\infty, \infty)$ and range is $(0, \pi)$. Today, I was surprised to notice that Mathematica treats it as an odd function, and yields its plot as given below:

How to reconcile this ? I welcome your comments.

Edit: I used: Plot[ArcCot[x], {x, -3, 3}] there to plot

Can you post the string you passed to Mathematica used to obtain this figure? — the_candyman, Sep 18 '20 at 09:28
I used: Plot[ArcCot[x],{x,-3,3}], there. I have also put it in my edit now. — Z Ahmed, Sep 18 '20 at 09:32
It depends on how you define $\cot^{-1}$ – as the inverse of $\cot$ on the interval $(0, \pi)$ or on the interval $(-\pi/2, \pi/2)$. — Martin R, Sep 18 '20 at 09:33
I am afraid it should not be left to choice. Similarly $\cos^{-1}(x)$ is also of mixed parity as $\cos^{-1}(-x)=\pi-\cos^{-1} x$. it is not an even function. — Z Ahmed, Sep 18 '20 at 09:36
The difference is explained here: https://mathworld.wolfram.com/InverseCotangent.html. — Martin R, Sep 18 '20 at 09:37

Martin R · Answer 1 · 2020-09-18T09:51:00.287

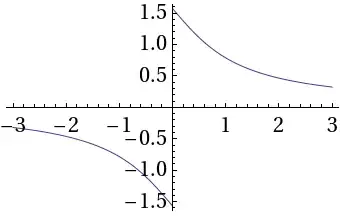
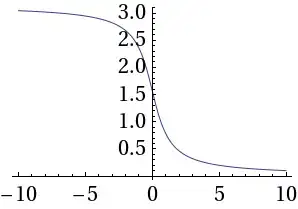
From Inverse Cotangent on Wolfram MathWorld:

There are at least two possible conventions for defining the inverse cotangent. This work follows the convention of Abramowitz and Stegun (1972, p. 79) and the Wolfram Language, taking $\cot^{-1}x$ to have range $(-\pi/2,\pi/2]$, a discontinuity at $x=0$, and the branch cut placed along the line segment $(-i,i)$.

This definition is also consistent, as it must be, with the Wolfram Language's definition of ArcTan, so ArcCot[z] is equal to ArcTan[1/z].

A different but common convention (e.g., Zwillinger 1995, p. 466; Bronshtein and Semendyayev, 1997, p. 70; Jeffrey 2000, p. 125) defines the range of $\cot^{-1}x$ as $(0,\pi)$, thus giving a function that is continuous on the real line $\Bbb R$.

The former definition is what Mathematica uses. Note that with that definition, $\cot^{-1}(0) = \pi/2$, so it is an odd function only if you exclude $x=0$ from the domain.

The latter definition satisfies $\cot^{-1}(-x)=\pi-\cot^{-1} x$ and is not an odd function.

Mathematica.SE provides some tricks, with some drawbacks – Vincenzo Tibullo Sep 18 '20 at 10:09 — Vincenzo Tibullo, Sep 18 '20 at 10:09

user · Answer 2 · 2020-09-18T09:42:55.857

0

We have that $\cot^{-1}(-x)$ is invertible only on suitable restrictions, in this case it seems Mathematica is considering the following definition

$$f(x)=\cot^{-1}(x): \mathbb R \to \left(-\frac \pi 2, \frac \pi 2\right)$$

that is also the definition used by Wolfram.

edited Sep 18 '20 at 09:42

answered Sep 18 '20 at 09:37

user

162,563

1

Mathematica is Wolfram. – Sep 18 '20 at 14:36
@YvesDaoust All is clear then! Thanks – user Sep 18 '20 at 14:51

score 0 · Answer 3 · answered Sep 18 '20 at 11:21

I think the Range of $f(x)=\cot^{-1} x$ as $(0,\pi)$ and hence the mixed parity of this function gets preference as then $f(x)$ is continuous in the its domain $(-\infty, \infty)$, specially at $x=0$. Then $\cot^{-1}(-x)=\pi-\cot (x)$.

In problem solving, for students, teachers and examiners this convention is most welcome for the sake of consistency. According to this $\cot^{-1} x$ function should look as below:

Why $\cot^{-1}x$ is an odd function in Mathematica

3 Answers3

Linked