Find the feasible region of a vector

Question

Consider two vector variables $x, y \in \mathbb{R}^n$. Both $x$ and $y$ are not given. We want to determine the region of $x$ that satisfies the constraints:

$$ \begin{cases} \|x - y\|_{\infty} \leq a, \\ \|y\|_{1} \leq b, \end{cases} $$ where $a, b \in \mathbb{R}^+$, and $\|\cdot\|_1$ and $\|\cdot\|_{\infty}$ denote the $L_1$ and $L_{\infty}$ norm.

My goal is to find a more explicit way to express the region of $x$ without relying on another vector $y$.

My thoughts:

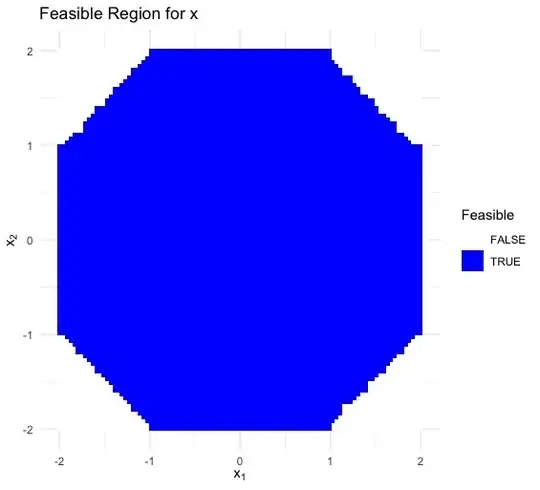
I did use R to solve this problem with $n=2, a=1, b=1$, and made the following graph in 2D space:

The first constraint is equivalent to $$ -a \leq x_i - y_i \leq a \quad \forall i. $$ Rearranging this, we have that $$ x_i - a \leq y_i \leq x_i + a \quad \forall i, $$ which implies that $$ |y_i| \leq \min(|x_i - a|, |x_i + a|). $$ In order to satisfy $$ \sum_{i=1}^n |y_i| \leq b, $$ I just have the following $$ \sum_{i=1}^n \min(|x_i - a|, |x_i + a|) \leq b. $$ As @RobPratt pointed out, this solution is wrong as it excludes $(x_1, x_2) = (0,0)$.

Answer 1

Given $$f(x) = a \|x\|_1 + b \|x\|_\infty$$ the convex conjugate is \begin{align} f^* (x) &= \sup_{y \in \mathbb{R}^n} \{ x^\top y - f(y) \} \\ &= \sup_{y \in \mathbb{R}^n} \{ x^\top y - a \|y\|_1 - b \|y\|_\infty \} \\ &= -\inf_{y \in \mathbb{R}^n} \{ -x^\top y + a \|y\|_1 + b \|y\|_\infty \} \\ \end{align} For fixed $x\in \mathbb{R}^n$, we want to minimize $$-\sum_{i=1}^n x_i y_i + a \sum_{i=1}^n |y_i| + b \max_{i=1}^n |y_i|$$

An equivalent linear programming (LP) problem is to minimize $$-\sum_{i=1}^n x_i y_i + a \sum_{i=1}^n z_i + b w$$ subject to \begin{align} z_i - y_i &\ge 0 &&\text{for $i\in\{1,\dots,n\}$} &(\alpha_i \ge 0) \\ z_i + y_i &\ge 0 &&\text{for $i\in\{1,\dots,n\}$} &(\beta_i \ge 0) \\ w - z_i &\ge 0 &&\text{for $i\in\{1,\dots,n\}$} &(\gamma_i \ge 0) \\ z_i &\ge 0 &&\text{for $i\in\{1,\dots,n\}$} \\ w &\ge 0 \end{align}

The LP dual problem is to maximize $0$ subject to \begin{align} -\alpha_i + \beta_i &= -x_i &&\text{for $i\in\{1,\dots,n\}$} &(\text{$y_i$ free}) \\ \alpha_i + \beta_i - \gamma_i &\le a &&\text{for $i\in\{1,\dots,n\}$} &(z_i \ge 0) \\ \sum_{i=1}^n \gamma_i &\le b && &(w\ge 0) \\ \alpha_i, \beta_i, \gamma_i &\ge 0 &&\text{for $i\in\{1,\dots,n\}$} \end{align}

Writing $x_i = \alpha_i - \beta_i$, $|x_i| = \alpha_i + \beta_i$, and $\gamma_i = \max(|x_i|-a,0)$ yields $$\sum_{i=1}^n \max(|x_i|-a,0) \le b$$

For $(n,a,b)=(2,1,1)$, this inequality matches your plot. But notice that your proposed inequality is too strong because, for example, it excludes $(x_1,x_2)=(0,0)$.

If the dual LP is feasible, the LP objective value is $0$. Otherwise, the primal LP is unbounded, with $\inf_{y\in \mathbb{R}^n} = -\infty$. Hence, the convex conjugate is $$f^*(x) = \begin{cases} 0 &\text{if $\sum_{i=1}^n \max(|x_i|-a,0) \le b$} \\ \infty &\text{otherwise} \end{cases}$$

As a check, this formula agrees with the convex conjugate for $|x|$ when $(n,a,b)=(1,1,0)$.

Answer 2

Imho, in linear programming the typical way of writing constraints is in the form of inequalities satisfied by linear expressions of the variables you iterate. Afaik this is also the typical form that numerical solvers expect. In your case: $-a\le x_i-y_i\le a$ for all $i$ plus $|y_1|+\dots+|y_n|\le b\,.$ The first constraint you mentioned in OP and is already of the desired form. The second constraint can be written as a sequence of $2^n$ mutually exclusive constraints \begin{align*} y_1+\dots+y_n&\le b\,,&&0\le y_1\,,\dots\,,0\le y_n\,,\\ &\vdots\\ -y_1-\dots-y_n&\le b\,,&& 0\le -y_1\,,\dots\,,0\le -y_n\,, \end{align*} each of which gives you one optimization problem. Solve these and then look through them to find the final optimal solution.