I've thought about the following question for a month, but I'm facing difficulty.
Question : Letting $S{^\prime}$ be the area of the inner pentagon made by the five diagonals of a convex pentagon whose area is $S$, then find the max of $\frac{S^{\prime}}{S}$.
$\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ $
It seems that a regular pentagon and its affine images would give the max. However, I don't have any good idea without tedious calculations. Can anyone help?
Update : I crossposted to MO.
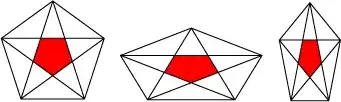
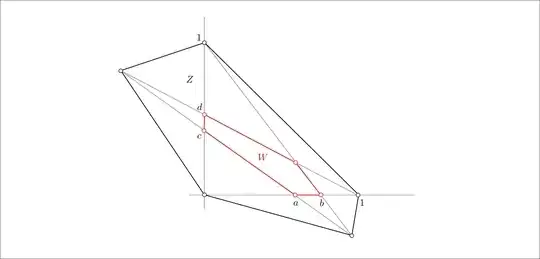
Denote by $z_i$ $(0\leq i\leq 4)$ the vertices of the large pentagon $Z$ and by $w_i$ the vertices of the small pentagon $W$. WLOG we may assume $$z_0=(0,0), \quad z_2=(1,0),\quad z_3=(0,1)$$ and $$w_3=(a,0), \quad w_4=(b,0),\quad w_1=(0,d),\quad w_2=(0,c)$$ with $$0<a<b<1,\quad 0<c<d<1,\quad d<{c\over a}<{1\over b}\ .$$
One then obtains $$z_1=\left({ba(1-c)\over a-bc}, {c(a-b)\over a-bc}\right),\quad z_4=\left({a(c-d)\over c-ad}, {dc(1-a)\over c-ad}\right),\quad w_0=\left({b(1-d)\over 1-bd}, {d(1-b)\over 1-bd}\right)\ .$$ This means that the moduli space ${\cal M}$ of such configurations up to affinity has dimension $4$. The values $a=c={3-\sqrt{5}\over2}\doteq0.381966$ and $b=d={\sqrt{5}-1\over2}\doteq0.618034$ correspond to regular pentagons $Z$ and $W$.
Further computation then gives $$2\>{\rm area}(Z)=1+{(b-a)c\over a- bc}-{a(d-c)\over ad-c}\>,\quad 2\>{\rm area}(W)={bd(2-b-d)-ac(1-bd)\over 1-bd}\ ,\tag{1}$$ and we are interested in the quantity $$t(a,b,c,d):={{\rm area}(W)\over {\rm area}(Z)}\ .$$ For regular pentagons $Z$ and $W$ one has $t={7-3\sqrt{5}\over2}\doteq0.145898$.
The expressions $(1)$ are complicated enough to forbid calculating partial derivatives of $t$. On the other hand it is easy to see that $\inf_{\cal M} t(a,b,c,d)=0$. As for the maximum of $t$ I simulated $10^7$ random such configurations with Mathematica and obtained the following optimal quintuple $(a,b,c,d,t)$: $$(0.383542, 0.619248, 0.381882, 0.618277, 0.14589)\ .$$ This supports the conjecture that $t$ is maximal for regular pentagons.
A complete solution is available at https://arxiv.org/abs/1812.07682
On the polygon determined by the short diagonals of a convex polygon, Jacqueline Cho, Dan Ismailescu, Yiwon Kim, Andrew Woojong Lee
Not a complete answer, and surely not elegant, but here's an approach. The idea is to consider "polygonal conics" in the following sense. Take the cone $K$ given by \begin{equation} K:\qquad x^2+y^2=z^2 \end{equation} and slice it with the plane $z=1$. We get a circle $\gamma$, and let's inscribe in this circle a regular pentagon, $P$ (The idea actually works with a regular $n$-gon with $n=2k+1$... should it be called $n$-oddgon?). The diagonals of this pentagon define a smaller pentagon $P'$. Let also $\gamma'$ be the circle in which $P'$ is itself inscribed in.
Let also $C,C',S,S'$ be the areas of $\gamma,\gamma',P,P'$ respectively. We have \begin{equation} \frac{C'}{C}=\frac{S'}{S} \end{equation} since all these areas depend only on the radiuses of $\gamma$ and $\gamma'$.
Let's now slice the initial cone and the cone $K'$ generated by the circle $\gamma'$ with a general plane \begin{equation} (x-x_0)\cos\theta+(z-z_0)\sin\theta=0 \end{equation} (Informally, it's the plane passing through $(x_0,0,z_0)$ and its normal vector lies in the plane $y=0$ and makes an angle $\theta$ with the $x$-axis).
We get two nested conics. Considering only the cases when these conics are ellipses, we can compute the ratio of their areas (area of the inner ellipse over area of the outer one) and one finds that the maximum of this value occurs when both are circles.
When only the inner conic is an ellipse, the ratio is zero.
Considering now the "pentagonal cones" obtained by extruding the original nested pentagons along the two cones $K$ and $K'$ and reasoning in a similar way as before, we have that the ratio between the areas of the nested "pentagonal conics" has a maximum when the pentagons are regular.
A problem with this approach is that I don't have a clue of what class of pentagons we are dealing with, as it may be too narrow to be of any real interest for the problem.
UPDATE: in the case of a pentagon, since five points in general position determine a conic, I guess we have covered all the possible cases.
Here is a partial answer.
Say point C of the large pentagon ABCDE is free to move, so long as the area does not change. We are curious what happens to the red area.
So C can move parallel to BD. As it does so, the red area increases on one side and decreases on the other side, due to CA and CE moving.
Consider CE, and the change in red area due only to CE as C moves by $\epsilon$ (parallel to BD). The point where CE crosses BD moves by $k \epsilon$, where $k$ is the constant ratio $m/n$ of the altitude $m$ from E to BD to the altitude $n$ from E to C's locus line. Indeed, the change in area is monotonic in the distance $s$ from B$'$ (the intersection of AD and CE) to BD, which itself is monotonic in the position of C.
The area of the red pentagon is affected in this way both by the change in area due to CE and by that due to CA, and therefore it is maximized when C is somewhere in the middle, and it is strictly concave in C's position.
Due to the symmetry of the regular pentagon, we can see the red area is at a local maximum in this case.
The question asks us to prove this is the global maximum, but I would guess an even stronger result, that this is the only local maximum, and even that the red area is strictly concave in the positions of the vertices (subject to constant area of the large pentagon).
If we could show that single-vertex area-preserving moves can transform any pentagon into any "nearby" one, with no vertex ever traveling far from its original position, then that would probably finish the proof of total strict concavity. It seems to be true, requiring $O(1/\epsilon)$ moves.
The area ratio $S’/S$ is always $k^2$ where $$k = {1-\sin(\pi/10) \over 1 + \cos(\pi/5)}.$$ $k$ is the ratio of the perimeter of the inner pentagon to the outer pentagon.
To see this, note that the inner pentagon appears to to be similar the outer pentagon but rotated by 180 degrees. Assume the outer pentagon is inscribed in a unit circle. Label the outer regular pentagon vertices as ABCDE with A at the top. Label the inner pentagon vertices as abcde but starting with a at the bottom. The triangles ACD and Acd are similar. It’s easily seen that the altitude of the Acd triangle is $1-\sin(\pi/10)$ and that of the ACD triangle is $1 + \cos(\pi/5)$. Thus, the ratio of cd to CD is $k$. Since cd and CD are sides of regular pentagons, the perimeter ratio must be $k$ and the area ratio must be $k^2$.
I leave the proof to others, but I assert that the following are invariant under any affine transformation:
The results have been checked with a MATLAB script that generates random affine transformations. Might add that these results should hold for other regular polygons except for the value of $k$. For example, $k = 1/3$ for a hexagon.
