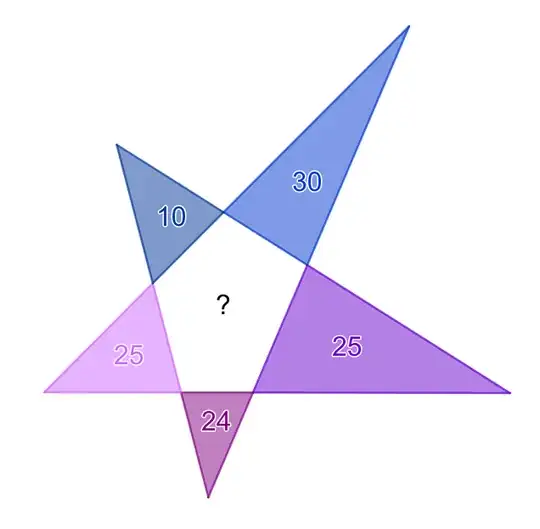
A star sign consists of five straight lines. It produces five big and five small total ten triangles and a pentagon. If areas of five small triangles are 30, 25, 24, 25 and 10 square unit respectively then what is the area of pentagon?
-
Image not appearing. – Deepak Oct 05 '20 at 16:04
-
I'm not sure if svg is supported. – player3236 Oct 05 '20 at 16:05
-
What have you tried so far? – KingLogic Oct 05 '20 at 22:54
-
I have finally obtained a solution, after an error of mine. Can you tell the origin of the problem ? – Jean Marie Oct 07 '20 at 08:42
1 Answers
(I am very indetebted to @Oscar Lanzi who has pinpointed an error of mine on barycentric coordinates signs, yielding a false conclusion).
1) First method
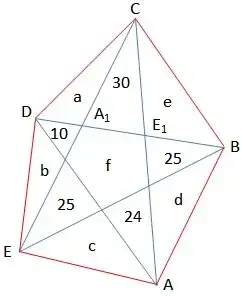
Fig.1.
Let us use the natural notations one can find on Fig. 1: $f$ for the central pentagon area, $a,b,c,d,e$ for triangular areas between spikes, etc.
We can write the following equations expressing common ratios of areas for triangles sharing the same bases. For example, for the first one, we have the equality of areas' ratios: $\dfrac{[ACB_1]}{[CDB_1]}=\dfrac{[EAB_1]}{[DEB_1]}$, i.e., $\dfrac{f+54}{10+a}=\dfrac{25+c}{b}$:
$$\begin{cases}b(f+54)&=&(25+c)(10+a)\\ c(f+35)&=&(24+d)(25+b)\\ d(f+55)&=&(25+e)(24+c)\\ e(f+34)&=&(30+a)(25+d)\\ a(f+50)&=&(10+b)(30+e)\end{cases}\tag{1}$$
To these equations, we can add the following alignment constraint of points $B,A_1,E_1$
$$\left|\underbrace{\begin{matrix} \ \ c+d+24\\ -(d+e+25)\\ \ \ e+f+80\end{matrix}}_{B} \ \ \underbrace{\begin{matrix}b+10\\a\\ 0\end{matrix}}_{A_1} \underbrace{\begin{matrix}d+25\\0\\ e\end{matrix}}_{E_1}\right|=0\tag{2}$$
using their (non-normalized) barycentrical coordinates with respect to triangle $CEA$.
Submitting system (1)+(2) (6 equations with 6 unknowns) to a symbolic Computer Algebra System gives many $6$-uples of "solutions", some with real values, some with complex values, only one of them being acceptable:
$$f=48.1691,$$
with:
$$a=26.1468, \ \ b=22.9426, \ \ c=39.8474, \ \ d=45.1259, \ \ e=47.9176.$$
2) 2nd method (that has my preference)
Let us take another direction giving the solution and, at the same time, an effective placement of the vertices.
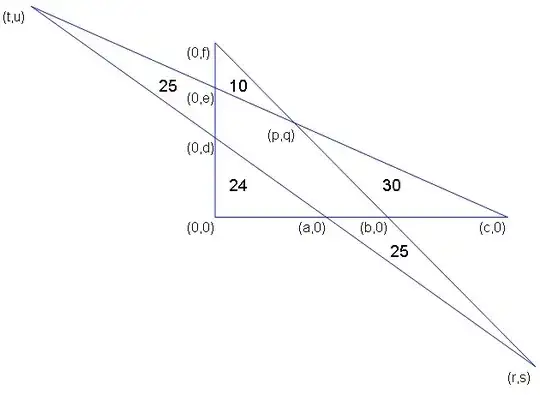
It is possible WLOG to assume that $AC \perp AD$ (by using a certain transvection which doesn't change areas ; see remark 1 below). Taking $A$ as the origin and $AC$ and $AD$ as axes of a coordinate system, we have $12$ unknowns $a,b,c,...$ (see fig. 2) with $11$ equations:
$$\begin{cases}\ \ \ ad&=&48\\ \ \ \ q(c-b)&=&60\\-s(b-a)&=&50\\-t(e-d)&=&50\\ \ \ \ p(f-e)&=&20 \end{cases} \ \ \ \ \ \ \begin{cases}\dfrac{p}{f-q}&=&\dfrac{b}{f}&=&\dfrac{r}{f-s}\\ \dfrac{q}{c-p}&=&\dfrac{e}{c}&=&\dfrac{u}{c-t}\\ \dfrac{-s}{r-a}&=&\dfrac{d}{a}&=&\dfrac{u}{a-t}\end{cases}$$
which are resp. the area constraints and the alignments constraints (or, more intuitively, equalities between slopes):
Fig. 2: A possible realization of the star. The points on the $x$ axis are: $(a=4;0), \ (b=6.216;0), \ (c=10.463;0)$, and on the $y$ axis $(0;d=12), \ (0;e=19.529), \ (0;f=26.438)$ with intersection points $p;q)=(2.894;14.126)$, $(r;s)=(11.521;-22.563)$ and $(t,u)=(-6.641;31.924).$
As there are $11$ equations and $12$ unknowns, we have to fix one of them; this is what we have done here by taking arbitrarily $a=4$. The solution given in Fig. 2 has been obtained by a CAS (as in the first method). It is worth mentionning the equations we have used expressing the values of the areas
Remarks:
Given fixed axes, there are two different kinds of transvections (also called shears) are: $\begin{pmatrix}1&\alpha\\0&1\end{pmatrix}$ or $\begin{pmatrix}1&0\\ \beta&1\end{pmatrix}$ for any $\alpha$ or any $\beta$. They preserve areas (and alignments, of course). They belong to the special linear group $SL_2$ of matrices with determinant $1$.
See as well: https://mathoverflow.net/q/143664
Slightly connected, the beautiful figures and properties in this article of Forum Geometricorum (Volume 16 (2016) 347–354) "Two Six-Circle Theorems for Cyclic Pentagons" authored by Grégoire Nicollet (http://forumgeom.fau.edu/FG2016volume16/FG201644.pdf)
Slightly connected too : Does the inner pentagon inside a Robbins pentagon $also$ have a rational area?
Here is a recent answer of mine where, as in the first solution, barycentrical coordinates are used in a pentagon.
Fig. 2 has a lot in common with the figure given by Christion Blatter here for a cousin issue I discovered today (2022-03-15).
- 88,997
-
I smell a rat. Did you check your system using five given areas of $1$, a central area of $\sqrt5$ and fill-in areas of $(1+\sqrt5)/2$? That case is a regular pentagram. – Oscar Lanzi Oct 06 '20 at 10:12
-
When I check it, the determinants do not line up. Barycentric coordinates can be negative, and you may have missed a sign in the $d+e+25$ and $a+b+10$ terms. – Oscar Lanzi Oct 06 '20 at 19:54
-
1@Oscar Lanzi You have pinpointed the error ! I have forgotten that the areas have to be considered as signed areas... I correct it... – Jean Marie Oct 07 '20 at 07:45