Is there an intuitive explanation why this probability is $1/2$? (robot dance)

Question

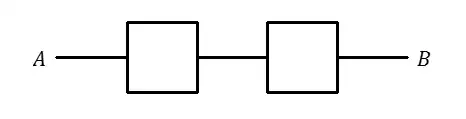
In the diagram, a robot starts at $A$ and moves right. Every time it reaches a fork (i.e. a point where it needs to choose among more than one direction), it chooses its next direction randomly, but does not turn back. It stops when it reaches either $A$ or $B$.

Let $P(B)=$ probability that the robot reaches $B$.

I have worked out that $P(B)=\frac12$, but my proof relies on calculation and is not intuitive.

Is there an intuitive explanation why $P(B)=\frac12$?

Proof that $P(B)=\frac12$

Let $M$ be the midpoint of the diagram. The probability that the robot reaches $M$ is:

$$\frac12+\left(\frac14\right)\left(\frac12\right)+\left(\frac14\right)^2\left(\frac12\right)+\left(\frac14\right)^3\left(\frac12\right)+\cdots=\frac{\frac12}{1-\frac14}=\frac23$$

(Explanation: The probability that it reaches $M$ as quickly as possible is $\frac12$. The probability that it walks $1.5$ loops around the left square then reaches $M$, is $\left(\frac14\right)\left(\frac12\right)$. The probability that it walks $2.5$ loops around the left square then reaches $M$, is $\left(\frac14\right)^2\left(\frac12\right)$. And so on, forming an infinite geometric series.)

If the robot reaches $M$, then the probability that it goes directly (shortest path) to $B$ is $\frac12$, and the probability that it does not go directly to $B$ is $\frac12$. If it does not go directly to $B$, then the probability that it eventually reaches $B$ is $1-P(B)$, by symmetry with the original question. So:

$$P(B)=\frac23\left(\frac12+\frac12\left(1-P(B)\right)\right)$$

$$\therefore P(B)=\frac12$$

(Generalization: If the diagram has $n$ squares, then the probability of reaching $B$ is $\frac{2}{2+n}$. This can be proved by induction.)

Context

A colleague of mine made up this question. I found it interesting because the answer is $\frac12$ and I can't seem to find an intuitive explanation. I am interested in such questions.

Answer 1

The only random choices that matter occur when the robot is moving vertically, and is deciding between continuing straight and turning horizontally. We ignore any decision where we approach the intersection horizontally, as both paths lead to the same next intersection.

If we number these nontrivial decisions, the odd-numbered decisions will always take place in the middle of the diagram, and the even-numbered decisions will take place on the outside edges, at the intersections that can directly lead to A or B.

Starting from either middle location on an odd-numbered decision, there is always one choice that will lead to the intersection near A as the next nontrivial choice, and one that will lead to the intersection near B. From there, there is one choice that will lead to the exit, and one that will lead back to a middle intersection.

Thus, on each pair of decisions, odd then even, there is one sequence of two choices that leads to an exit via A, one via B, and two sequences where the game continues. A and B are symmetrical, so the probability is 1/2.

Answer 2

This is a simulation of two coin tosses.

We have two outer forks: the ones connecting points $A$ and $B$ to their respective squares, and two inner forks: the ones that connect the two squares to each other.

If we start at point $A$, no matter which way we go around the square, we end up at the inner fork on the leftmost square. We flip a coin. If we get heads, we go to the second square where we end up at the fork that leads to point $B$. If we get tails, we stay on the left square and go to the fork that lead to $A$.

Therefore, if we get heads, we go to the fork at $B$ and if we get tails, we go to the fork at $A$.

If we are at either fork that leads to one of the points $A$ or $B$ and if we flip heads, we exit and if we flip tails, we go to an inner fork, where the game begins anew because from each of the inner forks, there is an equal probability to stay in the same square which leads to its exit, or to switch squares which leads to the other square's exit.

Therefore, we get the following outcomes:

$\text{HH}$, we go to point $B$
$\text{HT}$, we end up at an inner fork and the game begins again
$\text{TH}$, we go to point $A$
$\text{TT}$, we end up at an inner fork and the game begins again

We are equally likely to get $\text{HH}$ and $\text{TH}$ so there is an equal probability of exiting through either gate. If we get $\text{HT}$ or $\text{TT}$, it is the same as starting over again.

Answer 3

Idea

Let $G_n$ be the graph with $n$ squares (so your diagram is $G_2$). Let $P_0, P_1, \dots, P_n$ be (from left to right) points in between the squares but $P_0, P_n$ are the endpoints (so $P_0 = A$, $P_1 = M$, and $P_2 = B$ in your diagram).

For $0\le i < n$, let $X_{i}$ be the probability that, starting at $P_i$ and initially moving right, you hit $P_{i+1}$ before hitting $P_0$.

Then the total probability you want is $\prod_{i=0}^n X_{i}$.

It just so happens that $X_{0}X_{1}=\frac23 \frac34 = \frac24 = \frac12$ cancels out nicely to a half.

One can find that the general formula for $X_i$ is $X_i = \frac{i+2}{i+3}$, so the $n=2$ case is just a special case.

Answer 4

We can construct a bijection from tours ending at $A$ to tours ending at $B$. It will be described below.

Name the forks $P_1,M_1,M_2,P_2$ from left to right. Now, imagine a line $l$ passing through $A,P_1,M_1,M_2,P_2,B$. Whenever your tour takes you on a loop but above the line $l$, call it step $U$ and if it takes you below the line $l$, call it step $D$ and if you travel in the line segment $AP_1$ or $P_2B$, call it $E$ (entry/exit) and $M_1M_2$, call it $H$.

A tour $T$ can be represented as a word starting and ending with $E$. For example, $T=EUHUE$ is the tour that starts at $A$, goes to $P_1$, travels the first square above the line to $M_1$, goes from $M_1$ to $M_2$ and then, travels the second square above the line to $M_2$, and then exits at $B$.

Let $f$ be the first time the tour $T$ reaches point $M_1$ or $M_2$ through an U or D step and then decides to take to stay on the current square with a D or U step, we will introduce an intermediary $H$ step from $M_1$ to $M_2$, thereby changing the word from $UD$ or $DU$ to $UHD$ and $DHU$ respectively. Similarly, for the first time $T$ reaches $M_1$ or $ M_2$ through an $U$ or $D$ and goes from $M_i$ to $M_j$ and then takes $D$ or $U$ respectively, we will change the word from $UHD$ or $DHU$ to $UD$ and $DU$. Notice that this will take a tour ending at $A$ to one ending at $B$ and vice versa.

The only tours that are yet unmapped are ones that are of the form $(UHUDHD)^k$, $(DHDUHU)^k$ and $UHU(DHDUHU)^k$ or $DHD(UHUDHD)^k$. The first two will end at $A$ and the last two will end at $B$. This is clearly a bijection.

$\textbf{Remark:}$ Not all words in the alphabet $U,H,D$ with a prefix and suffix $E$ will correspond to a tour.

Answer 5

Here's a straightforward approach that avoids infinite series and instead uses a Markov chain. Let the states be $\{A,1,2,3,4,B\}$, where $A$ and $B$ are terminal, the numbered states correspond to arriving at the forks vertically, and we start in state $2$. Let $p_i$ be the absorption probability into state $B$, given current state $i$. By first-step analysis (conditioning on the first step out of each state), we obtain linear equations \begin{align} p_A &= 0 \\ p_1 &= \frac{1}{2}p_A + \frac{1}{2}p_2 \\ p_2 &= \frac{1}{2}p_1 + \frac{1}{2}p_4 \\ p_3 &= \frac{1}{2}p_1 + \frac{1}{2}p_4 \\ p_4 &= \frac{1}{2}p_3 + \frac{1}{2}p_B \\ p_B &= 1 \end{align} Solving yields $$p_A = 0,\ p_1 = \frac{1}{4},\ \color{red}{p_2 = \frac{1}{2}},\ p_3 = \frac{1}{2},\ p_4 = \frac{3}{4},\ p_B = 1$$

Answer 6

The problem is equivalent to a robot moving from in graph $A-M_1-M_2-M_3-M_4-B$ ($M_1,M_2,M_3,M_4$ represent the forks) with new redefined rules added:

1. Left half and right half are symmetric.
2. When robot reach $M_2$ from the left or $M_3$ from the right, it has choices.
3. When robot reach $M_2$ from the right, it must move right; when robot reach $M_3$ from the left, it must move left.

Robot starts at $A$, it must move to $M_1$, then it must move to $M_2$ so we can say it starts at $M_2$.

When it starts at $M_2$, probability $1/2$ it moves to $M_1$ from the right $(1)$, probability $1/2$ it moves to $M_3$ from the left, but then by rule 3, it must continue to move to $M_4$ from the left $(2)$.
From $(1)$ and $(2)$, by symmetry (determined by lastest position and lastest movement), we conclude $P(\textrm{robot reachs B})=P(\textrm{robot reachs A})=1/2$