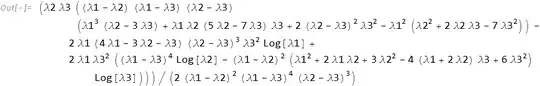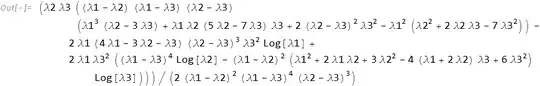I want to calculate $$ \mathbb{E} \left[ \frac{X_1}{\sum_{i=1}^{N} X_i} \right] $$ when $ X_i $'s are independent (but not identical) exponential distribution.
I found solution when $N=2$ in this post: Expected value of $X/(X+Y)$.
I also know that if $X_i$'s are i.i.d. exponential distribution, $ \frac{X_1}{\sum_{i=1}^{N} X_i} $ follows beta-distribution.
But I want a general case solution.
How can I solve this problem? Does this variable follow well-known distribution?
Thank you.
Some thoughts.
Using the identity $$\frac{1}{u} = \int_0^\infty \mathrm{e}^{-s u}\, \mathrm{d} s,$$ we have \begin{align*} \mathbb{E} \left[ \frac{X_1}{\sum_{i=1}^{N} X_i} \right] &= \mathbb{E} \left[\int_0^\infty X_1\mathrm{e}^{- s(\sum_{i=1}^{N} X_i)}\,\mathrm{d} s \right] \\ &= \int_0^\infty \mathbb{E}\left[X_1\mathrm{e}^{- s(\sum_{i=1}^{N} X_i)}\right]\,\mathrm{d} s \\ &= \int_0^\infty \mathbb{E}\left[X_1\mathrm{e}^{-sX_1}\right] \prod_{i=2}^N\mathbb{E}\left[\mathrm{e}^{-s X_i}\right]\,\mathrm{d} s\\ &= \int_0^\infty \frac{\lambda_1}{(s + \lambda_1)^2} \prod_{i=2}^N \frac{\lambda_i}{s + \lambda_i}\,\mathrm{d} s. \end{align*}
Ex. 1: Expected value of $X/(X+Y)$,
$N = 2, \lambda_1 = 1, \lambda_2 = 2, \mathbb{E} \left[ \frac{X_1}{X_1 + X_2} \right] = \int_0^\infty \frac{1}{(s+1)^2}\frac{2}{s + 2}\,\mathrm{d} s = 2 - 2\ln 2$.
Ex. 2: $\lambda_i = \lambda, \forall i$
$$\mathbb{E} \left[ \frac{X_1}{\sum_{i=1}^{N} X_i} \right] = \frac{1}{N}.$$
Here is a more analytical approach.
We want to find $E(Z)$ where
$$Z=X_1/\sum_{i=1}^n X_i=X_1/ \left(X_1+\sum_{i=2}^n X_i\right)=X_1/(X_1+Y)$$
where the $X_i$ random variables are independent exponential distributions all with different parameters:
$$X_i \sim \text{Exponential}(\lambda_i)$$
and $Y$ has a hypoexponential distribution with parameters $\lambda_2, \ldots,\lambda_n$.
The pdf of $Y$ is
$$\left(\prod_{i=2}^n \lambda_i\right) \sum_{i=2}^n \left(e^{-y \lambda_i} /\prod_{\substack{j=2 \\j\neq i}}^n {(\lambda_j-\lambda_i)}\right)$$
The mean of $Z$ can be found with the following:
$$\mu=\int_0^\infty \int_0^\infty \frac{x_1}{x_1+y} e^{-x_1 \lambda_1} \lambda_1 \left(\prod_{i=2}^n \lambda_i\right) \sum_{i=2}^n \left(e^{-y \lambda_i}/ \prod_{\substack{j=2 \\j\neq i}}^n {(\lambda_j-\lambda_i)}\right) dy dx_1$$
$$=\left(\prod_{i=1}^n \lambda_i\right) \sum_{i=2}^n \frac{1}{\prod_{\substack{j=2 \\j\neq i}}^n {(\lambda_j-\lambda_i)}} \int_0^\infty \int_0^\infty \frac{x_1}{x_1+y} e^{-x_1 \lambda_1-y \lambda_i} dy \ dx_1$$
$$= \left(\prod_{i=1}^n \lambda_i\right) \sum_{i=2}^n \frac{1}{\prod_{\substack{j=2 \\j\neq i}}^n {(\lambda_j-\lambda_i)}} \frac{\lambda_i-\lambda_1 (1+\log(\lambda_i/\lambda_1))}{\lambda_1(\lambda_1-\lambda_i)^2}$$
Addition
To answer the comment: Find the mean when the first $k$ $\lambda$'s are not equal but the last $n-k$ $\lambda$'s are all equal to $\mu_{k+1}$ which doesn't equal any of the first $k$ $\lambda$'s.
I have no desire to perform the needed algebra by hand so I'm using Mathematica as in my other answer.
(* Set values for n and k *)
n = 6;
k = 3;
(* Obtain mean when no lambdas are equal *)
μ = Product[λ[i], {i, 1, n}] Sum[(λ[i] - λ[1] (1 + Log[λ[i]/[1]]))/
(Product[If[j == i, 1, λ[j] - λ[i]], {j, 2, n}] λ[1] (λ[1] - λ[i])^2), {i, 2, n}];
(* Take the limit of μ as λ[k+1],...,λ[n] -> m = λ[k+1] *)
μ = (Limit[μ, Table[λ[i] -> m, {i, k + 1, n}]]) /. m -> λ[k + 1]
As a check set some $\lambda$ values and perform some simulations:
lambdas = {1, 2, 3, 4, 4, 4};
μ /. Table[λ[i] -> lambdas[[i]], {i, 1, k + 1}] // N]
(* 0.341686 *)
SeedRandom[12345]
nSims = 10000000;
(* Random samples from n exponentials )
data = Transpose[Table[RandomVariate[ExponentialDistribution[lambdas[[i]]], nSims],
{i, 1, n}]];
( Find x[1]/(x[1]+...+x[n] for each simulation )
z = #[[1]]/Total[#] & /@ data;
( Mean of simulated z values )
Mean[z]
( 0.341589 *)
2nd addition
If you have any of the $\lambda$ values that are equal, then probably the more efficient way to obtain the associated mean (that also doesn't require one to take limits) is to use @RiverLi 's answer with Mathematica (or Maple or MATLAB). Here is a Mathematica implementation of that:
λ = {3, 2, 5, 5, 5}
Integrate[(λ[[1]]/(s + λ[[1]])^2) Product[λ[[i]]/(s + λ[[i]]), {i, 2, Length[λ]}],
{s, 0, ∞}, Assumptions -> Table[λ[[i]] > 0, {i, 1, Length[λ]}]]
(* -(5/72) (708 + 400 Log[2] + 675 Log[3] - 1075 Log[5]) *)
That code also works symbolically:
λ = {λ1, λ2, λ3, λ3, λ3};
Integrate[(λ[[1]]/(s + λ[[1]])^2) Product[λ[[i]]/(s + λ[[i]]), {i, 2, Length[λ]}],
{s, 0, ∞}, Assumptions -> Table[λ[[i]] > 0, {i, 1, Length[λ]}]]
One possibility that is at least suggestive is to generate the means for various values of $n$ and then look for a unifying pattern.
Using Mathematica (but I'm sure Maple and MATLAB can do this in a similar manner) one can produce a table of means for various values of $n$:
Format[\[Lambda][i_]] := Subscript[\[Lambda], i]
Format[x[i_]] := Subscript[x, i]
m = Table[{n, Mean[TransformedDistribution[x[1]/Sum[x[i], {i, 1, n}],
Table[x[i] \[Distributed] ExponentialDistribution[\[Lambda][i]], {i, 1, n}]]]},
{n, 2, 4}];
TableForm[m]
One can see that the denominator has the form
$$\left(\prod _{i=2}^n (\lambda (1)-\lambda (i))\right) \prod _{i=1}^{n-1} \prod _{j=i+1}^n (\lambda (i)-\lambda (j))$$
The next step would be to determine the form of the numerator for a general value of $n$.