I am working on a robotics calibration problem and I've run into a geometry problem that I'm sure has a solution, but I'm not sure how to tackle it.
We have a square and we want to find the size of the square. We know the lengths of BE, CE, and DE. In particular the length of BE is the same as CE so BE = CE.
We want to compute the length of AB or any other side of the square given those two lengths.
Does anyone have an idea of how to go about doing that?
Thanks for giving it a look!
Seems straightforward enough. Let the side length be $\ell$. Drop a perpendicular from E to AD and call its length $y$. And suppose BE = CE = $a$ and DE = $b$. Then you have two equations in the unknowns $\ell$ and $y$: $$ y^2 + (\ell / 2)^2=b^2 $$ and $$ (\ell - y)^2 + (\ell / 2)^2 = a^2. $$ That's enough information to determine $\ell$.
This is a work in progress to take advantage of Latex
$Y^2+(L/2)^2=B^2$ solved for Y becomes
$$Y=\frac{\sqrt{4B^2-L^2}}{2}$$
Then solving the second equation $(ℓ−y)2+(ℓ/2)2=a2$ for L we get:
$$L =\frac{ 2(\sqrt{5 A^2 - Y^2)}}{5} + 2 Y$$
In both cases we just kept the positive half because both Y and L are positive.
Plugging the first equation into the second equation we get:
$$L =\frac{ 2\sqrt{5 A^2 - (\frac{\sqrt{4B^2-L^2}}{2})^2)}}{5} + 2 (\frac{\sqrt{4B^2-L^2}}{2})$$ $$L =\frac{ 2\sqrt{5 A^2 - (\frac{\sqrt{4B^2-L^2}}{2})^2)}}{5} + \sqrt{4B^2-L^2}$$ $$L=2A^2+\frac{4}{5}\sqrt{4V^2-L^2}$$
Solving that for L we get two answers:
$$L=\frac{2}{41}(25A^2-4\sqrt{41B^2-25A^4})$$ $$L=\frac{2}{41}(4\sqrt{41B^2-25A^4}+25A^2)$$
Checking with some real world numbers from the CAD constraints solver:
In this case A = 3 and B = 2
$$L=\frac{2}{41}(25(3)^2-4\sqrt{41(2)^2-25(3)^4})$$ $$L=\frac{2}{41}(225-4\sqrt{-1861})$$
:/
$$L=\frac{2}{41}(4\sqrt{41B^2-25A^4}+25A^2)$$ $$L=\frac{2}{41}(4\sqrt{-1861}+225)$$
:/
So I've for sure gone off the rails somewhere
Let's do a quick sanity check by plugging the values from the CAD constraints solver into our initial equations to make sure they are correct.
$$Y=\frac{\sqrt{4B^2-L^2}}{2}$$ $$Y=\frac{\sqrt{4(2)^2-(3.458)^2}}{2}$$ $$Y=\frac{\sqrt{-3.95}}{2}$$
Which isn't right :p
BUT plugging the values into $Y^2+(L/2)^2=B^2$ gives us 4=4 which is right, so that first solve is not right.
Solving it the other way works though. If we solve for L we can get
$$L = 2\sqrt{B^2 - Y^2}$$
Which holds up when we plug in our values.
Then if we check the other one we find the same thing.
$$L =\frac{ 2(\sqrt{5 A^2 - Y^2)}}{5} + 2 Y$$ checked against our values gives:
3.458 = 4.66 which is not right. Checking the original
$$(ℓ−y)2+(ℓ/2)2=a2$$
That one works. Let's try solving that equation for Y instead of L
$$Y=L-\frac{1}{2}\sqrt{4A^2-L^2}$$
Checking that with our values gives the right answer. Our two equations are:
$$L = 2\sqrt{B^2 - Y^2}$$ and $$Y=L-\frac{1}{2}\sqrt{4A^2-L^2}$$
Plugging those together gives four options of which
$$L=\frac{\sqrt{A^2+\sqrt{-A^4+6A^2B^2-B^4}+B^2}}{\sqrt{2}}$$
Seems to be the correct one.
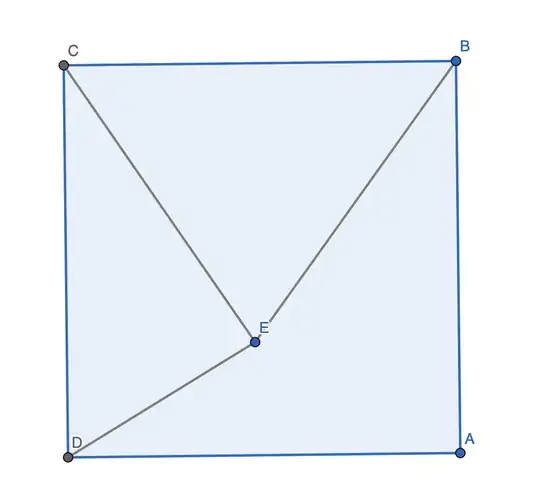
A solution for any E in square ABCD
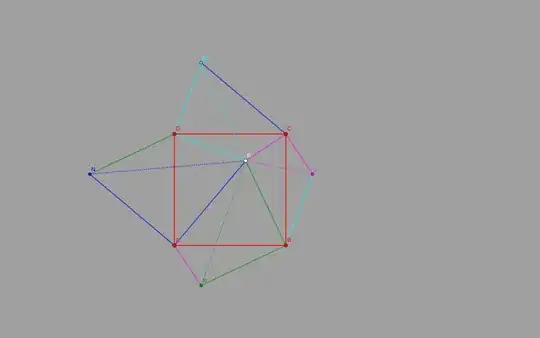
Picture has the triangles the square is composed of appended to the sides.
Let a (blue) b (green) c (magenta) d (cyan) be the distances from any interior point E to the vertices A B C D of the square.
The total area $O$ of the octagon is twice the area of the square.
There are four mono color (blue, green, magenta, cyan) orthogonal equilateral triangles contributing:
(1) $$\frac{a^2+b^2+c^2+d^2}{2}$$
to the total area of the octagon.
The remaining contributing four three color triangles have one of the sides (shown dotted) a distance multiplied by $\sqrt{2}$.
The side lengths $$(x,y,z)$$ of these four triangles are equal to $$(a,\sqrt{2}b,c)$$ $$(b,\sqrt{2}c,d)$$ $$(c,\sqrt{2}d,a)$$ $$(d,\sqrt{2}a,b)$$ and their areas can be computed by Heron's formula:
(2) $$\sqrt{s(s-x)(s-y)(s-z)}$$ where $$s = \frac{x+y+z}{2}$$
So now we can sum up total octagon area $O$ and the square side is:
(3) $$\sqrt(\frac{O}{2})$$
But: $d$ is a function of $(a,b,c)$ :
(4) $$d(a,b,c)=\sqrt{a^2-b^2+c^2}$$
[where one chooses a b c correctly a>=b>=c]
This is not hard to prove [draw lines through E parallel to square sides and use Pythagoras].
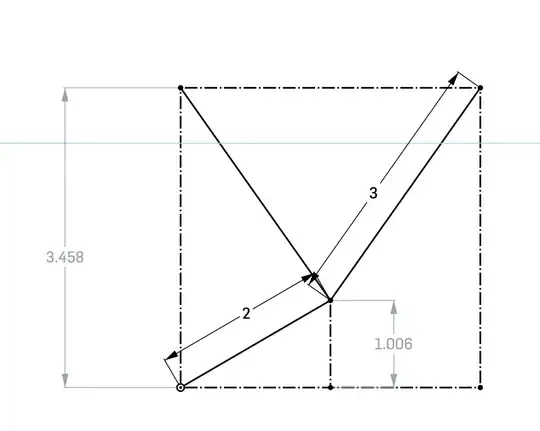
Below Julia code tests an OP @BarSmith answer example case where $CE=3$ and $DE=2$ giving expected square side rounded $3.458$.
Combining (1) and (2) and (3) and (4) allows to explicitly write a formula (as is implicitly done in code).
# Heron formula for triangle area
# given triangle sides
function H(a,b,c)
s = (a + b + c) / 2
return sqrt(s * (s - a) * (s - b) * (s - c))
end
side length of square ABCD given distances a b c d
from interior point E to vertices
function L(a,b,c,d)
# 4 orthogonal equilateral triangles
surface =
((a^2 + b^2 + c^2 + d^2) / 2) +
# 4 extra tricolor triangles with one side * sqrt(2)
H(a, sqrt(2) * b, c) +
H(b, sqrt(2) * c, d) +
H(c, sqrt(2) * d, a) +
H(d, sqrt(2) * a, b)
# surface is twice square surface
# side length is square root
return sqrt(surface / 2)
end
distances d to vertex D of square ABCD
given distances a b c
from interior point E to vertices A B C
D(a, b, c) = sqrt(a^2 - b^2 + c^2)
side length of square ABCD given distances a b c
from interior point E to vertices A B C
a >= b >= c
function L(a,b,c)
return L(a, b, c, D(a, b, c))
end
3 3 2 example
a = 3
b = 3
c = 2
d = 2
println(L(a,b,c))
exit(0)
$ julia Julia/abcde.jl 3.457507202786114
