How to prove that a line segment will intersect the same number of grid points before and after being moved parallely?

Question

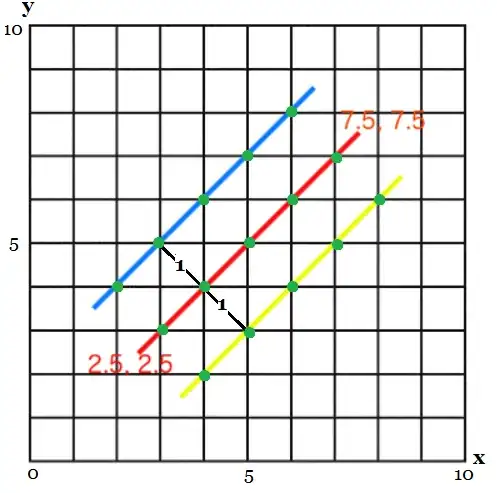
I almost ran out of characters for the question title so I couldn't clarify as much as I wanted to but here goes:

A grid point is simply a point where both the $x$ and $y$ values are in $\mathbb{Z}$.

Assume I have a line segment defined by the two grid points $P_1$ and $P_2$ where $P_1 = (x_1, y_1)$ and $P_2 = (x_2, y_2)$.

I then calculate the normal vector to that line segment so I can move it exclusively parallel:

$d_x = x_2 - x_1$

$d_y = y_2 - y_1$

$\vec{k} = \begin{bmatrix}-d_y\\d_x\end{bmatrix}$

I then calculate the unit vector of that normal vector and use it to move the line segment in its direction like so (where $m$ is the magnitude of movement and $n$ is the unit vector of the normal vector to the line segment)

The magnitude of movement ($m$) is also in $\mathbb{Z}$ ie it's a whole number multiplier.

$T_x = \vec{n}_x \cdot m$

$T_y = \vec{n}_y \cdot m$

$P_1' = (round(x_1 - T_x), round(y_1 - T_y))$ and $P_2' = (round(x_2 - T_x), round(y_2 - T_y))$

In my setup, it is guaranteed that the new points are also in $\mathbb{Z}$ because they get rounded.

I think it may be needed to replace rounding with something else, such as rounding based on which value preserves the slope because I am confident the slope cannot be allowed to change for this to be true, so for now assume the function "round()" does just that: rounds the output to the points that preserve the slope

So simply put, I have a line segment defined by two integer points and I move it parallely to two new also integer points. I want to prove that if the line segment before the translation was intersecting with $N$ grid points then it will remain to do so after the translation as described above.

Picture for illustration: green points are intersections with the grid.

Answer 1

I will focus on answering your question as you phrased it in the end, and as demonstrated in your picture, as I am not sure the discussion around rounding is correct/relevant.

Applying a parallel shift to your line means your applying a translation $T$ to all the points on the line. Let $l$ denote your initial line, and $l'$ be the translated line. If $(a, b)\in l$, then $T((a, b)) = (a + \Delta_x, b+\Delta_y)$ for some $\Delta_x$ and $\Delta_y$. In particular, if $T$ takes a lattice point on $l$ to a lattice point on $l'$, then $\Delta_x$ and $\Delta_y$ are integral. Thus, every lattice point on $l$ is mapped to a (unique) lattice point on $l'$. The same holds for the inverse $T^{-1}$ of $T$, so the lattice points on $l$ are in bijection with those on $l'$, i.e., they are equinumerous, as desired.

The above essentially shows that the number of lattice points on a line between two lattice points depends only on the slope of said line. You might be interested in the fact that the number of lattice points on a line segment between lattice points $(a, b)$ and $(c, d)$ is given by $\gcd(c−a,d−b)+1$, see here for a proof.