Prove $O_{ABC}O_{BCD}O_{CDA}O_{DAB}$ is concyclic

Question

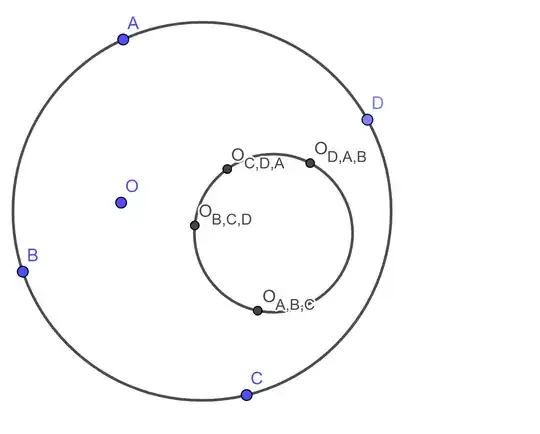
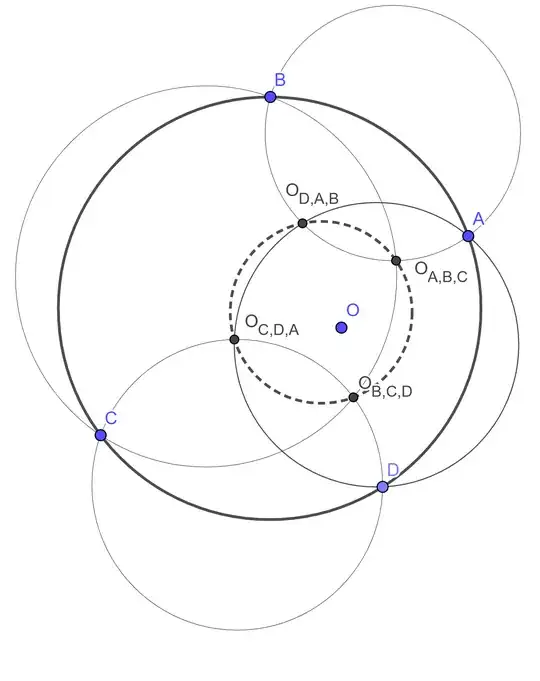
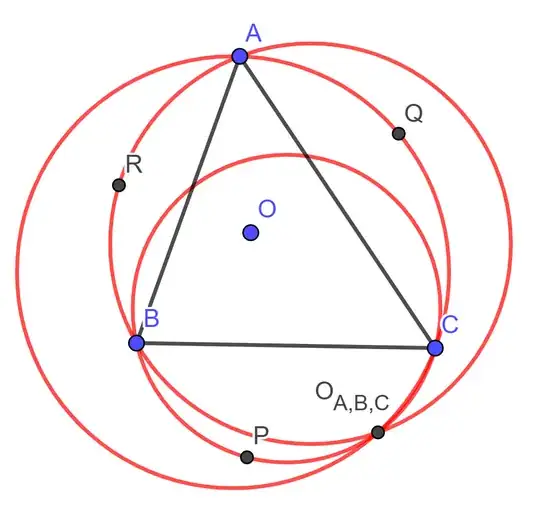
For 4 points $O,A,B,C$, let the reflection of $O$ across $BC,CA,AB$ be $P, Q, R$, resp. Then the circumcircles of $BCP,CAQ,ABR$ must intersect at a point, denote this point as $O_{ABC}$.

I'm interested in proving the following:

Let $ABCD$ be a concyclic quadrilateral, then $O_{ABC}O_{BCD}O_{CDA}O_{DAB}$ is concyclic.

I tried to prove it by angle chasing, but it seems not easy to do so.

Answer 1

$A,B,O_{DAB},O_{ABC}$ are on the circle through $A,B$ and the reflection of $O$ across $AB$.

Similarly

$ABO_{DAB}O_{ABC},BCO_{ABC}O_{BCD},CDO_{BCD}O_{CDA},DAO_{CDA}O_{DAB}$ are concyclic.

so the problem reduces to Miquel's six circle theorem