Proof of Miquel's six circle theorem

Question

Theorem

Miquel's six circle theorem states that if in the following all cocircularities except the last one are satisfied, then the last one is implied.

In words: if $ABCD$ lie on a circle, and $ABYZ,BCXY,CDWX,DAZW$ likewise, then $XYZW$ lie on a circle (or a line) as well.

Motivation

The Wikipedia section on this is really short and does reference some books, but no online resources. So I think it would be nice to have various proofs for this theorem available here. I'll provide one (moved to an answer so it can be vote-sorted, too), but I want to know how other people with a different background would tackle this. So I make this an alternative-proof question.

Answer 1

Apply circle inversion (https://en.wikipedia.org/wiki/Inversive_geometry) with respect to any circle with centre $A$. It maps circles through $A$ to straight lines and other circles to circles. Thus, the problem is reduced to a simpler problem where there is a given triangle $B’D’Z’$ and points $C’$, $W’$, $Y’$ on lines $B’D’$, $D’Z’$, $Z’B’$, respectively, and we know that circumscribed circles around $\triangle B’C’Y’$ and $\triangle D’C’W’$ intersect in a point $X’$. All that is left to prove is that points $X’,Y’,Z’,W’$ belong to the same circle. But this is a direct consequence of a (much simpler) Miquel’s theorem for a triangle (https://en.wikipedia.org/wiki/Miquel%27s_theorem).

Note: in the proof above, $B’$ is the image of $B$ by the chosen circle inversion, and similar for $C’, D’$ etc.

Answer 2

Since the motivation of the question was the lack of online resources, the theorem in question is Théorème I in Miquel's paper Théorèmes sur les intersections des cercles et des sphères, Journal de mathématiques pures et appliquées v3 (1838), 517-522.

It's proven via angle chasing. As a reading note, the symbol $d$ refers to a right angle, so $2d$ is the angle $\pi$. The figures are at "Planche III"

(Theorem IV in the same paper states that stereographic projection takes circles on a sphere to circles on a plane. The textbook Ostermann-Wanner, Geometry by Its History claims this is a rediscovery of a theorem by Ptolmey.)

The same volume also contains another paper by Miquel.

Answer 3

Sidler, Géométrie projective, Chapter 8, examines several Euclidean geometry problems from the standpoint of projective geometry.

For the Miquel Theorem, Sidler considers the Desargues involutions on the line at infinity induced by cyclic quadrangles. These involutions exchange the circular points $I,J$. He shows that the involution for $WXYZ$ is the composition of the involutions for $ADWZ,ABCD,BCXY$ and therefore also swaps $I,J$.

If there's interest I can provide more info. (I'm also not sure whether you're looking for original proofs, or are ok with existing proofs from the literature)

Answer 4

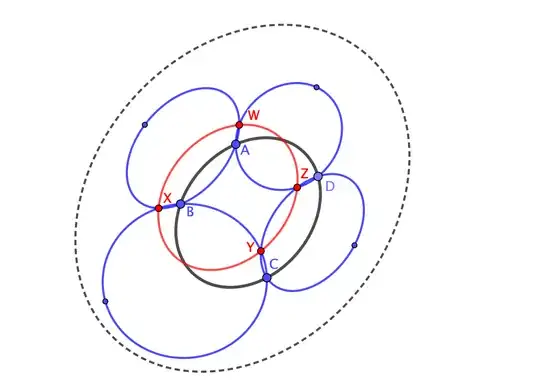
Originally this proof was part of the question statement.

The proof I know uses the cross ratio in the complex plane. Consider your points as complex numbers. Then four points are cocircular (or collinear) if their cross ratio is real (as I will discuss in more detail below). So the circle $\bigcirc ABCD$ leads to the equation

$$(A,B;C,D)=\frac{(A-C)(B-D)}{(A-D)(B-C)}\in\mathbb R$$

and the other circles lead to similar equations. Furthermore, a different order of points on a circle leads to a different equation, too. Choosing the orders of points appropriately you can multiply all the cross ratios to obtain

$$ (A,C;B,D)\cdot(A,Y;Z,B)\cdot(C,Y;B,X)\cdot(C,W;X,D)\cdot(A,W;D,Z)=\\ \frac{\color{#00f}{(A-B)}\color{#090}{(C-D)}}{\color{#c00}{(A-D)}\color{#0cc}{(B-C)}}\cdot \frac{\color{#c0c}{(A-Z)}\color{#660}{(Y-B)}}{\color{#00f}{(A-B)}(Y-Z)}\cdot \frac{\color{#0cc}{(C-B)}(Y-X)}{\color{#09c}{(C-X)}\color{#660}{(Y-B)}}\cdot\\ \frac{\color{#09c}{(C-X)}\color{#900}{(W-D)}}{\color{#090}{(C-D)}(W-X)}\cdot \frac{\color{#c00}{(A-D)}(W-Z)}{\color{#c0c}{(A-Z)}\color{#900}{(W-D)}}=\\ -\frac{(Y-X)(W-Z)}{(Y-Z)(W-X)}=-(Y,W;X,Z) $$

so if all the original cross ratios were real, then so is the final one. Usually I'd formulate this in terms of homogeneous coordinates, writing $2\times2$ determinants instread of the differences, and taking the point at infinity from $\mathbb{CP}^1$ into account, but that's not all that relevant to this question here.

I learned this proof from Prof. Richter-Gebert at university, and his book Perspectives on Projective Geometry has a variation of this in section 18.5. There he describes a circle as a conic through the ideal circle points $[1:\pm i:0]$ but otherwise the approach is essentially the same: multiply all inputs and cancel terms.

Cross ratios and cocircularity

The underlying relationship between real cross ratio and cocircularity can be explained like this: Consider $(A-C)$ as the vector pointing from $C$ to $A$. Use

$$(A-C)=r_{CA}\exp\left(i\varphi_{CA}\right)$$

to express this vector in polar coordinates. Now

$$\frac{A-C}{B-C}=\frac{r_{CA}}{r_{CB}} \exp\left(i\left(\varphi_{CA}-\varphi_{CB}\right)\right)$$

has an argument (angle) which depends on the difference of the angles of the individual vectors. And for the whole cross ratio you get

$$\frac{(A-C)(B-D)}{(A-D)(B-C)}=\frac{r_{CA}r_{DB}}{r_{DA}r_{CB}} \exp\left(i\left(\varphi_{CA}+\varphi_{DB}-\varphi_{DA}-\varphi_{CB}\right)\right)$$

which is real iff

$$\varphi_{CA}+\varphi_{DB}-\varphi_{DA}-\varphi_{CB}\equiv0\pmod\pi\\ \varphi_{CA}-\varphi_{CB}\equiv \varphi_{DA}-\varphi_{DB}\pmod\pi$$

which translates to $\angle ACB\equiv\angle ADB$: two points $C$ and $D$ form the same (oriented) angle with the line segment $AB$. So this is essentially just a form of the inscribed angle theorem. As a special case, if the differences on both sides of the equation are zero, the four lines are collinear.

Answer 5

There is a nice correspondence between Miquel's problem in 2D and configurations of planar slices of a sphere.

See Miquel's Six Circles in 3d and also Problem 11 and its solution on this page.

The statements in the references are respectively

Let a cuboid be placed in 3d in such a way that seven of its vertices belong to a sphere. Then the eighth vertex also belongs to the same sphere.

and

If seven vertices of a hexahedron lie on a sphere, then so does the eighth vertex.

The statements can be generalized to quadrics, e.g. ellipsoids. See this question and its answer.

The 2D version of the quadrics generalization can be expressed as a relationship between six conics that are in double contact with a seventh conic as seen in the following figure. The seventh conic has the dashed outline.

This can also be interpreted as a hyperbolic Miquel's theorem, where the figure is a Beltrami-Klein model of hyperbolic space with the dashed ellipse as the "absolute" aka line at infinity, and the other six ellipses are hyperbolic circles in this model.

But the figure can also be interpreted as a projection of a quadric and six planar sections. The outer dashed ellipse is the silhouette of the quadric, and the inner ellipses are intersections of planes with the quadric.