Is it better to hire $1$ fast barista vs $2$ slower baristas?

Question

This is another math puzzle I heard today.

Consider a M/M/K queue (https://en.wikipedia.org/wiki/M/M/c_queue) in a cafe. Lets say the cafe has a rule that each queue is FIFO (first in first out), each customer can only order one coffee at a time and then leave the queue with the coffee.

Consider two such cafes:

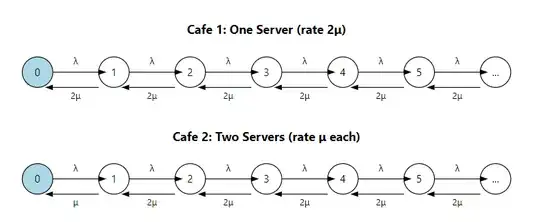
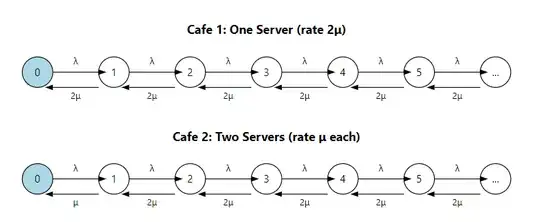
• Cafe 1: There is $1$ barista that finishes orders at rate = $2 \mu$
• Cafe 2: There are $2$ baristas that each finish orders at a rate of $\mu$

Provided customers arrive at the same rate in both cases (i.e. all other conditions in both cafes are identical), can we expect that in the long run, on average (i.e. in multiple simulations) :

• both cafes will finish the same number of orders?
• the average queue throughout the day will be similar for both cafes ?
• customers on average will wait for the same amount of time to receive their orders?

Naively, I think the answer is yes?
Essentially, the rate is just scaled up to compensate for the missing barista?

---

This my attempt to visualize the queue as a birth-death process. The only difference between the two scenarios is that when there is only one person in the queue, the rate changes (1 fast barista vs 1 slow barista). Perhaps this is the difference?

Answer 1

Simulation will involve knowing the "Arrival times" , "Wait times" , "Distributions" , all of which will impact the outcome.

Here is my Intuition :

Let the Cafe1 Barista take 1 minute to make 1 coffee , while the Cafe2 Barista takes 2 minutes.

• When there are no customers :
  -- both are idle , both are same
• When there is one customer :
  -- C1 will finish faster , customer will wait less ( 1 minute )
  -- C2 will finish slower , customer will wait more ( 2 minutes ) , one Barista will be idle.
• When there are two customers :
  -- both are finish at same time.
  -- C1 customer will wait $(1+2)/2$ average : less
  -- C2 customer will wait $(2+2)/2$ average : more
• When there are 200 customers :
  -- both are finish at same time.
  -- C1 customer will wait $(1+2+\cdots+200)/200$ average
  -- C2 customer will wait $(2+2+4+4+\cdots+200+200)/200$ average

Thus we see that when we have large number of customers , wait times are same , finish times are same.
While when we have less number of customers , C1 is faster , wait times are lesser.

Hence when we have various numbers over the time , C1 will be approximately same as C2 , though it will have a slight advantage.

Basically Intuition is that C1 has slight advantage because idle time in C1 is less : there is 1 Barista idling. C2 has slight disadvantage because idle time in C2 is more : there is 2 Barista idling.

ADDENDUM :

We have not accounted for the "wages" : When C1 Barista charges more , then trade-offs will change.

We have not accounted for a lot of other tings too , which naturally makes this analysis incomplete.

Answer 2

Looking at the two Markov chains side by side shows what the difference is.

The two systems are identical when there are $0$ customers or when there are $2$ more customers in the system, because in those cases the transitions from that state have identical rates. Intuitively:

• When there are no customers, it doesn't matter how many baristas you've got and how fast they are.
• When there are two or more customers, a fast barista and two slow baristas are both working at the same rate, in total, so the two systems are, again, identical.

When there is $1$ customer in the system, then the only difference shows up: the fast barista will finish that customer's coffee twice as quickly.

The two systems are identical in one respect: in both cases, we should measure load as $\rho = \frac{\lambda}{2\mu}$, because that determines the maximum amount of customers they can handle. In both cases:

• if $\rho < 1$, the Markov chain is positive recurrent (and will return to $0$ in expected finite time);
• if $\rho = 1$, the Markov chain is null recurrent (and will return to $0$ in expected infinite time, but still with probability $1$);
• if $\rho > 1$, the Markov chain is transient (and with positive probability will never return to $0$).

If $\rho < 1$, we can compute the stationary distribution: it is $$1-\rho, \rho(1-\rho), \rho^2(1-\rho), \dots, \rho^k(1-\rho), \dots$$ for the first cafe and $$\frac{1-\rho}{1+\rho}, 2\rho \frac{1-\rho}{1+\rho}, 2\rho^2 \frac{1-\rho}{1+\rho}, \dots, 2\rho^k \frac{1-\rho}{1+\rho},\dots$$ for the second cafe. It follows that the average length of the queue is longer by a factor of $\frac{2}{1+\rho}$ in the second cafe.

From the customer's point of view, there are two main differences:

1. No matter how long the line is, the actual time it takes to make that customer's order is longer in the second cafe. That's because at that point, you're simply comparing it being made by a fast vs. a slow barista.
2. The average length of the line is going to be longer in the second cafe.