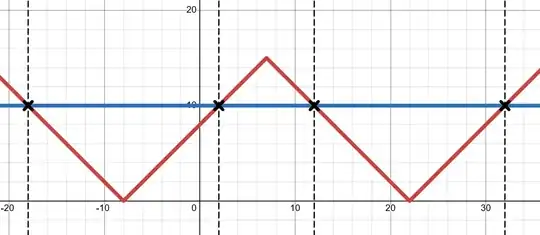
The problem
Solve the equation: $||x-7|-15|=10$
My idea
I took 2 cases:
Case $1$: $|x-7|-15=10\implies |x-7|=25\implies$
(a) $ x-7=25\implies x=32$
(b) $ x-7=-25\implies x=-18$
Case $2$: $|x-7|-15=-10\implies |x-7|=5\implies$
(a) $x-7=5\implies x=12$
(b) $ x-7=-5\implies x=2$
So the solution I got were $x=32,-18,12,2$
I'm not sure if taking the cases like this is a correct reasoning.
\impliesto get $\implies$ instead of using => – jjagmath Sep 04 '24 at 14:16