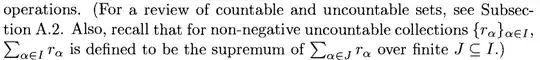Weird definition of discrete random variable - How do you define a sum over an uncountable set?

Question

After this huge eye opener Discrete Random Variables May Have Uncountable Images (cf https://math.stackexchange.com/questions/4957619/discrete-random-variables-may-have-uncountable-images-almost-surely-countab) I checked my probability textbooks on their definitions of discrete random variable

From Rosenthal - A First Look at Rigorous Probability Theory

Translating this to random variables, I guess it's saying...

Let $X$ be a random variable.

(

To relate to laws I guess :

1. Let $\mathscr B$ be the Borel $\sigma$-algebra on $\mathbb R$ or however it's called - I forgot. Then its law is $L_X:\mathscr B \to \mathbb R$, $L_X(B):=P(X \in B)$.

2. And then any Borel 'probability' measure $\mu$ on $\mathbb R$ is any measure on the measurable space $(\mathbb R, \mathscr B)$ w/ $\mu(\mathbb R)=1$. And then $\mu$ is actually the law of some random variable $X$ in some probability space $(\Omega, \mathcal F, \mathbb P)$

)

$X$ is discrete if $\sum_{x \in \mathbb R} P(X=x) = P(X \in \mathbb R)$,

or in law language

$X$ is discrete if $\sum_{x \in \mathbb R} L_X\{x\} = L_X(\mathbb R)$,

where I guess we might view the event $ \{ X \in \mathbb R \} $ as $\bigcup_{x \in \mathbb R} \{ X = x \}$ to show countable additivity or something.

And then the exercise is an equivalent definition is

There is a countable set $S \subseteq \text{im}(X) \subseteq \mathbb R$ with $P(X \in S) = 1$ i.e. $P(X \notin S) = 0$.

or in law language

There is a countable set $S \subseteq \text{im}(X) \subseteq \mathbb R$ with $L_X(S) = 1$ i.e. $L_X(S^C) = 0$.

Question : But the initial definition is kinda weird since you can sum over a countable set only right?

Answer 1

This usually requires some discussion because it's not a part of usual sum definitions from calculus that everyone knows, but you can sum nonnegative values over uncountable sets by defining $$\sum\limits_{x \in S} P(x) = \sup \left\{ \sum\limits_{x \in I} P(x) \,\middle|\, I \subset S, I \text{ finite}\right\}$$ Rosenthal notes this in passing in §1.2: