To preface: Is anyone aware of information on a distribution similar to the Inverse Gaussian but for the case where the time-dependent process's position follows a Student's T distribution? If so, are you aware if this function is available in any programming languages, especially in its CDF form?
Consider a stochastic process involving arrival (or hitting) times for entities undergoing Brownian motion with drift. If the drift rate is known but the underlying variance is variable, what is a good way to model the arrival time distribution? I did some research on this site and in a few books but did not find any resources. I made an attempt to model the Brownian motion with variable variance as a hierarchical distribution as follows. (The work below will be similar to the derivation of the Inverse Gaussian distribution, which is covered in many places, but the approach I followed is from here.)
Brownian motion with drift, where position at time $t$ is $X_t$, with drift rate $\mu$, infinitesimal variance $\sigma^2$, and $W_t\sim\mathcal{N}(0,t)$, can be modeled as follows.
$$X_t=\mu t+\sigma W_t$$
For the distribution of $X_t$, I chose to use a gamma distribution to model the precision $(\tau^2=1/\sigma^2)$ owing to the natural conjugacy relationship (additionally it appears to be a decent model for the true distribution I am working with). For parameters $\alpha$ and $\beta$, we know that after marginalization we will obtain a t-distribution with $\nu=2\alpha$ (with $\nu\ge3$ for finite variance); we will then set $\beta$ based off a variance estimator (I skip this step here).
$$X_t\mid\tau^2\sim\mathcal{N}(\mu t,t/\tau^2), \;\tau^2\sim\mathcal{G}(\alpha,\beta)$$
We marginalize the conditional distribution to find the density for $X$ (and define $Y=\tau^2$).
\begin{align} p(X=x)&=\int_0^\infty p(X=x\mid Y=y)p(Y=y)dy\\ &=\int_0^\infty\left(\frac{\sqrt{y}}{\sqrt{2\pi t}}e^{-(x-\mu t)^2 y/2t}\right) \left(\frac{\beta^{\nu/2}}{\Gamma(\nu/2)}y^{\nu/2-1}e^{-\beta y}\right)dy\\ &=\frac{\beta^{\nu/2}}{\Gamma(\nu/2)\sqrt{2\pi t}}\int_0^\infty y^{(\nu/2+1/2)-1}e^{-((x-\mu t)^2+2t\beta) y/2t}dy\\ &=\frac{\Gamma((\nu+1)/2)\beta^{\nu/2}}{\Gamma(\nu/2)\sqrt{2\pi t}}\left(\frac{2t}{(x-\mu t)^2+2t\beta}\right)^{\nu/2+1/2} \end{align}
(The integration for the last line results from the kernel of the gamma distribution.) This is a t-distribution which we aim to invert to obtain the distribution for arrival time. We begin with the derivative of the distribution function and substitute $T=\sqrt{(x-\mu t)^2/\beta t}$ along with $dT=1/\sqrt{\beta t}dx$.
\begin{align} dP&=\frac{\Gamma(\nu/2+1/2)\beta^{\nu/2}}{\Gamma(\nu/2)\sqrt{2\pi t}}\left(\frac{2t}{(x-\mu t)^2+2t\beta}\right)^{\nu/2+1/2}dx\\ &=\frac{\Gamma(\nu/2+1/2)}{\Gamma(\nu/2)\sqrt{2\pi}}\left(\frac{2}{T^2+2}\right)^{\nu/2+1/2}dT\\ &=\frac{\Gamma(\nu/2+1/2)}{\Gamma(\nu/2)\sqrt{2\pi}}\left(\frac{2}{T^2+2}\right)^{\nu/2+1/2}\frac{dT}{dt}dt\\ &=\frac{\Gamma(\nu/2+1/2)}{\Gamma(\nu/2)\sqrt{2\pi}}\left(\frac{2}{\frac{(x-\mu t)^2}{\beta t}+2}\right)^{\nu/2+1/2}\left(\frac{1}{2}\sqrt{\frac{\beta t}{(x-\mu t)^2}}\frac{-2\mu\beta t(x-\mu t)-\beta(x-\mu t)^2}{\beta^2t^2}\right)dt\\ &=\frac{\Gamma(\nu/2+1/2)}{2\Gamma(\nu/2)\sqrt{2\pi}}\left(\frac{2\beta t}{(x-\mu t)^2+2\beta t}\right)^{\nu/2+1/2}\left(\frac{x+\mu t}{\sqrt{\beta t^3}}\right)dt \end{align}
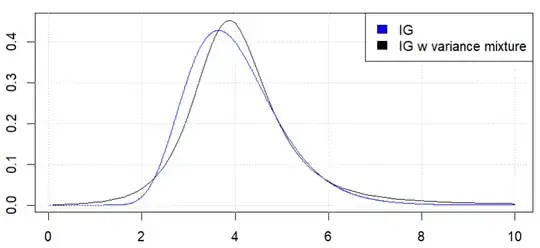
This resulting distribution for arrival time (which I will refer to as the Inverse T or IT distribution for brevity) is the equivalent to an Inverse Gaussian (IG) distribution but if the Brownian motion's distribution at each time interval was a t-distribution rather than normal. I plotted the density function for the IT below in comparison with the IG using similar parameters for each (same position $x$, drift rate $\mu$, and overall distribution variance (functions of $\sigma^2$ for IG and $\beta$ for IT); for IT, degrees of freedom $\nu=3$). The IT distribution has a few desired properties (fat tails, right skew), and one particularly surprising property (expected value appears to increase slightly with increasing standard deviation, a property not present in the IG).
To recap, I am hoping someone would be familiar with this distribution and point me toward some useful resources. (Also, it is entirely possible I made a mistake in my math that could use correction.)