How long will it take for Polya's Urn to have the same Ratio as it had in the Beginning?

Question

Recently I learned that in Polya's Urn starting with $m$ red balls and $n$ blue balls ... as time goes to infinity, the ratio of red to blue balls converges to its initial ratio (Polya's urn model - limit distribution). Intuitively, I interpret this as follows:

• At $t=0$, the ratio of red to blue balls is $\frac{m}{n}$
• At $t=\infty$, the ratio of red to blue balls is also $\frac{m}{n}$

This brings me to my question:

Define $t$ as the time between $(0, \infty)$, at which the ratio of red to blue balls is again $\frac{m}{n}$:

$$ \min \{ t > 0 \colon \frac{R(t)}{B(t)} = \frac{m}{n} \} $$

What is the probability distribution of $t$, $P(T=t)$ ? In other words, how long will it take for Polya's Urn to first return to the same ratio of balls as it had in the beginning?

I thought that perhaps this could be modelled as a asymmetrical Random Walk, and thus we could treat this problem as a Hitting Time Distribution question (e.g. First Hitting Time Distribution of a Random Walk with Drift follows an Inverse Gaussian Distribution), but I was not sure how to set this up.

Instead, I tried to find out the Expected Value and Variance of $t$.

1) Expected Value: Start with

$$m = \text{initial number of red balls}$$ $$n = \text{initial number of blue balls}$$

The total number of balls at the start is:

$$N = m + n$$

In Polya's Urn model, the ratio of red to blue balls at t = ∞ converges to the initial ratio:

$$\lim_{t \to \infty} \frac{R(t)}{B(t)} = \frac{m}{n}$$

where $R(t)$ and $B(t)$ are the numbers of red and blue balls at time $t$.

To find when we expect the ratio to be $m:n$ again, we need to consider the expected number of balls added before this occurs. Let's call this as x.

We can define a logical relationship as:

$$\frac{m+x\frac{m}{m+n}}{n+x\frac{n}{m+n}} = \frac{m}{n}$$

Solving this equation:

$$\frac{m(m+n)+xm}{n(m+n)+xn} = \frac{m}{n}$$

$$m(m+n)+xm = m(m+n)+xm$$

$$E(T) = x = m+n = N$$

Thus, it seems as if once you after $N$ turns have passed such that $N$ equals the original number of balls - the ratio of red to blue balls after $N$ turns will also be the same as the ratio of red to blue balls at the start.

2) Variance I am unsure how to calculate the Variance . I started doing this:

$$P(\text{red at t}) = \frac{X_t}{X_t + Y_t}$$

$$E(T^2) = \sum_{t=1}^{\infty} t^2 \cdot P(T=t)$$

But I am not sure how to continue.

Can someone please show me how to derive the variance for the time in this problem? And is it possible to get a PDF (rather PMF) for the time?

Notes:

• https://observablehq.com/@cmoog/polya-urn-simulation

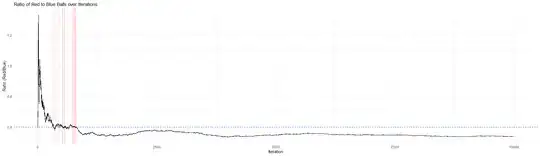
Edit: Some Visualizations of an Urn that starts with a ratio of 3:5 and how it returns to its original ratio (I can include the R code if anyone is interested):

Answer 1

The quantity $T:=\min\left\{ t>0 : \frac {R(t)}{B(t)} = \frac m n\right\}$ can have infinite expectation:

Polya's Urn model can be understood as a certain monotone random walk $X(t)=(R(t),B(t))$ on $\mathbb{Z}^2$ where the question is when do we hit the line through the origin again that we start on. In the simple case $m=n$, the line in question is the line $R=B$.

Let's focus on this case. We will define a strongly dependent random walk $Y$ on $\mathbb{Z}$ as follows: $Y$ starts at $0$. If $R=B$, $Y$ will increase by $1$ if and only if a red ball is added to the urn, otherwise it will decrease by $1$. If $R>B$, then the likelihood of adding a red ball is $\frac R {R+B}> \frac 1 2$, so we can define $Y$ to increase by $1$ with a probability of exactly $\frac 1 2$ but only if a red ball was added. Otherwise it decreases by $1$. Similarly if $R<B$, the likelihood of adding a blue ball is larger than $\frac 1 2$ so we can make it that $Y$ decreases by $1$ with probability $\frac 1 2$, but only if a blue ball was added. Otherwise it increases by $1$. Note that $Y$ is just a random walk on $\mathbb{Z}$ that either increases or decreases by $1$ with a probability of $\frac 1 2$ each. This random walk is well-understood. In particular, it is known that the walk is so-called recurrent null, that is, it will come back to its starting point with probability 1, but the expected time until it does is infinite.

Since both walks are symmetric in exchanging blue and red, we can assume the first ball is red and $Y$ starts out in the positive. Now we know the expected time $Y$ returns to $0$ is infinite, so we just have to argue, that $X$ hits the line $R=B$ later than that. For instance, it is sufficient to show that $Y\leq R-B$ until it returns to $0$. However this is just true by definition, because $Y$ can only ever increase by $1$ if $R-B$ does as well and else it decreases by $1$, which is the most decrease that can happen within a single step to $R-B$ as well.

Answer 2

This is just a long comment, rather than a full answer.

Let $X=\min \left\{ t > 0 \colon \frac{R(t)}{B(t)} = \frac{m}{n} \right\}$. Also let's assume that $m$ and $n$ are coprime. Then $P(X=t)=0$ when $t$ is not divisible by $m+n$. Let's look at $P(X\le k(m+n))$.

Consider the event $S_t$ defined as $R(t(m+n))=(t+1)m$ and $B(t(m+n))=(t+1)n$ simultaneously. Then $P(X\le k(m+n))=P(S_1\cup \cdots\cup S_k)$.

We can use inclusion-exclusion for this, but we first need to find the "intersection probabilities". That is, we need to find $P\left(\cap_{i\in I} S_i\right)$, where $I\subseteq \{1,\ldots,n\}$. If we order $I$, then this is $\prod_{r=1}^{|I|}P(S_{I_r}|S_{I_1},\ldots,S_{I_{r-1}})$. But because only the most recent state matters, this simplifies to $\prod_{r=1}^{|I|}P(S_{I_r}|S_{I_{r-1}})$

This actually isn't too hard to find given the probability given here because it's as if we are just recalculating the required probabilities with new parameters. If I didn't mess anything up (in terms of how many balls there are at the end of the relevant set, and how many are getting added), it comes out to $$\prod_{r=1}^{|I|}\binom{(m+n)(I_r-I_{r-1})}{m(I_r-I_{r-1})}\frac{(m(I_{r-1}+1))^{\overline{m(I_r-I_{r-1})}}(n(I_{r-1}+1))^{\overline{n(I_r-I_{r-1})}}}{((m+n)(I_{r-1}+1))^{\overline{(m+n)(I_r-I_{r-1})}}}$$ where $I_0$ is understood to be $0$. This simplifies kind of nicely to $$\frac{m^{\overline{mI_{|I|}}}n^{\overline{nI_{|I|}}}}{(m+n)^{\overline{(m+n)I_{|I|}}}}\prod_{r=1}^{|I|}\binom{(m+n)(I_r-I_{r-1})}{m(I_r-I_{r-1})}$$ Here, $I_{|I|}$ is just the largest value of $I$.

Of course, now we'd want to actually work with this in the inclusion-exclusion formula...