Context and introduction
I was playing with complex number sequences $Z_n=r_n\omega^n=u_n+iv_n$ represented in space and realized that it's always possible to associate up to 48 naturally symmetric curves associated to the initial curve by doing binary manipulations and shifts on the coordinates.
$$\vec{X}_n=u_n\hat{i}+v_n\hat{j}+f(|Z_n|)\hat{k}=(u_n,v_n,w_n)$$
The reason why I mention the number 48 here in the introduction will be more clear in this text later.
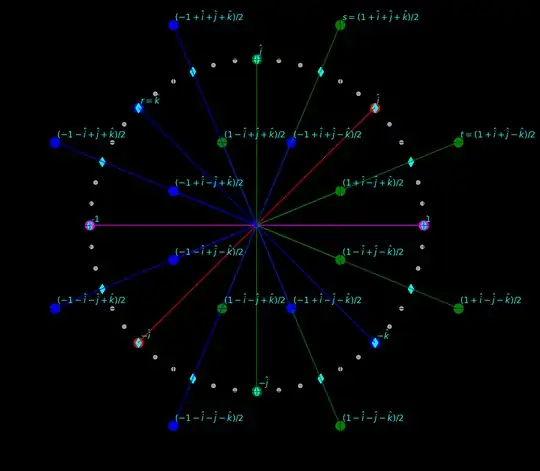
Now because of doing research to find references where binary counting is present in the emergence of symmetries of geometric figures in space, I was introduced to the idea of the 24-cell, and the geometry related to it. I feel I have the motivation to finally understand quaternions by playing with this object. So I started doing some experiments starting with one of the basic projections of the 24-cell by doing this basic construction where these questions arise:
My attempt to find the logic in the Binary tetrahedral group
Q1: I can't understand why the elements of the group are "order 6" for $s$ and $t$ and "order 3" or "order 4" for the other binary combinations. I understand it refers to the order of the elements, as in the least number of times an action must be applied to the element to get the identity element, but can't understand how is done here. (see edit at the end on this question)
Q2: In this construction, we will find that
$$r^2=s^3=t^3=-1$$
Why is this important in projections, I imagine is some normalization but can't find it's motivation as a general idea.
(edit)
Reading the answer from R.J I realize where my confusion might be. In the graph from Wikipedia says $r=k$ , and I ended up mixing the projection data with the quaternions.
$$r^2=(-1)=e^{\pi i}$$
So $r$ is an order 4 generator? It's a 4-gon generator in it's projection and generates the axis of the projection by:
$$r=e^{\frac{\pi i}{2}}=e^{\frac{2\pi i}{4}}=i$$
But they are not simple complex numbers, they are quaternions, so $i$ here cant be just a complex number.
$$s=\frac{1}{2}(1+i+j+k)$$
$$t=\frac{1}{2}(1+i+j-k)$$
So both are order 6 generators because $s^6=t^6=1$
And I solved for $j$ and $k$ fixing $r=i$ and considering $r^2=s^3=t^3=-1$ to see the shape of the projection :
$$r=i$$
$$s=e^{\frac{\pi i}{3}}=\frac{1}{2}+i\frac{\sqrt{3}}{2}$$
$$t=e^{\frac{-\pi i}{3}}=\frac{1}{2}-i\frac{\sqrt{3}}{2}$$
- Note we get the imaginary golden ratio Imaginary Golden Ratio
Solving for $j$ and $k$ we get:
$$k=s-t=i\sqrt{3}$$
$$s+t=1+i+j$$
$$j=s+t-1-i=1+i\sqrt{3}-1-i=i(\sqrt{3}-1)$$
$$(i,j,k)=(i,\sqrt{3}i,(\sqrt{3}-1)i)$$
- Trying to check if this manipulations arrive to something useful I realize that these expressions have Hurwitz expansion as a continued fraction:
$$\hat{s}=\frac{1}{2}(1+i+\sqrt{3}i+\sqrt{3}i-i)=\frac{1}{2}+\sqrt{3}i= \frac{\sqrt{13}}{2}e^{i tan^{-1}(2 \sqrt{3})}$$
$$\hat{t}=\frac{1}{2}(1+i+\sqrt{3}i-\sqrt{3}i+i)=\frac{1}{2}+i=\frac{\sqrt{5}}{2}e^{i tan^{-1}(2)}$$
- Are $\hat{s}$ and $\hat{t}$ used in some projection?
Q3: Considering this why, are $r,s,t$ special ?
Initial attempt to understand the projection in the complex plane
$$n \geq 0 \in \mathbb{N}$$
$$\omega=e^{\frac{2\pi i}{T_o}}$$
(+1)- Order 1
- (+1) (Magenta Axis) $$1=\omega^0=\omega^{T_o n}=e^{2\pi i n}$$
(-1)- Order 2
- (-1) - Label (2) - (Magenta Axis)
$$-1=\omega^{\frac{T_o}{2}(2n+1)}=e^{i \pi (2n+1)}$$
6 - Order 4 - These are the 6 faces of a cube
Cartesian coordinates - orthogonal axis $$(u_n,v_n,w_n)=u_n\hat i+v_n\hat j+w_n\hat k$$
| Binary | Expression | Order | Axis |
|---|---|---|---|
| 000 | $\hat i = e^{\frac{2\pi i}{8}} = e^{\frac{\pi i}{4}} = \omega^{\frac{T_o}{8}}$ | 4 | Red Axis |
| 001 | $-\hat i = e^{\frac{2\pi i}{8} + i\pi} = e^{\frac{\pi i}{4} + i\pi} = \omega^{\frac{T_o}{8}}\omega^{\frac{T_o}{2}(2n+1)}$ | 4 | Red Axis |
| 010 | $\hat j = e^{\frac{2\pi i}{4}} = e^{\frac{\pi i}{2}} = \omega^{\frac{T_o}{4}}$ | 4 | Green Axis |
| 011 | $-\hat j = e^{\frac{2\pi i}{4} + i\pi} = e^{\frac{\pi i}{2} + i\pi} = \omega^{\frac{T_o}{4}}\omega^{\frac{T_o}{2}(2n+1)}$ | 4 | Green Axis |
| 100 | $r=\hat k = e^{3\frac{2\pi i}{8}} = e^{\frac{3\pi i}{4}} = \omega^{\frac{3T_o}{8}}$ | 4 | Blue Axis |
| 101 | $-\hat k = e^{3\frac{2\pi i}{8} + i\pi} = e^{\frac{3\pi i}{4} + i\pi} = \omega^{\frac{3T_o}{8}}\omega^{\frac{T_o}{2}(2n+1)}$ | 4 | Blue Axis |
8 Order 6 -> $+ 1 \pm a \hat i \pm b \hat j \pm c \hat k$ - Green
| Binary | Expression | Order |
|---|---|---|
| 0000 | $s=(1 + \hat i + \hat j + \hat k)/2 $ | 6 |
| 0001 | $t=(1 + \hat i + \hat j -\hat k)/2 $ | 6 |
| 0010 | $(1 + \hat i - \hat j + \hat k)/2 $ | 6 |
| 0011 | $(1 + \hat i - \hat j - \hat k)/2 $ | 6 |
| 0100 | $(1 -\hat i + \hat j + \hat k)/2 $ | 6 |
| 0101 | $(1 -\hat i + \hat j -\hat k)/2 $ | 6 |
| 0110 | $(1 -\hat i -\hat j + \hat k)/2 $ | 6 |
| 0111 | $(1 -\hat i -\hat j -\hat k)/2 $ | 6 |
8 Order 3 -> $- 1 \pm a \hat i \pm b \hat j \pm c \hat k$ - Blue
| Binary | Expression | Order |
|---|---|---|
| 1000 | $(-1 + \hat i + \hat j + \hat k)/2 $ | 3 |
| 1001 | $(-1 + \hat i + \hat j -\hat k)/2 $ | 3 |
| 1010 | $(-1 + \hat i - \hat j + \hat k)/2 $ | 3 |
| 1011 | $(-1 + \hat i - \hat j - \hat k)/2 $ | 3 |
| 1100 | $(-1 -\hat i + \hat j + \hat k)/2 $ | 3 |
| 1101 | $(-1 -\hat i + \hat j -\hat k)/2 $ | 3 |
| 1110 | $(-1 -\hat i -\hat j + \hat k)/2 $ | 3 |
| 1111 | $(-1 -\hat i -\hat j -\hat k)/2 $ | 3 |
So I made some code to test if I was correctly decoding the projection and made some plots with it in 2D.
Q4: I made this plot using a $T_o=48$ because it looked like a sufficient enough resolution to encode the 24 elements in the projection into the unit circle as 16 unique angles using an expression of the form $r_n e^{\frac{2\pi i}{48}k}$ for $k=3n$ , being $r_n$ the appropriate modulus for the correspondent element of the projection. I was trying to construct this but realized that might be already done and have a common expression for $r_n \in \mathbb{C} $ that produces a phase shift along with the radius. Maybe this a way to get the Cayley Graph? Is 48 special in this context?
About Q1 (edit)
I understand what the order of a group is (The number of elements in the group) , and how is different to the order of an element (as the least number of times that an action must be applied to go to the identity element) . But in this group I can't see how is being done, and why are those the order of the elements on the cases of order 6, 3 and 4.
To help potential answers to the question to know the starting level I add context some basic context and definitions.
Definition of a group
Definition:
•A group is a non-empty set $G$ together with a rule that assigns to each pair g, h of elements of $G$ an element $g ∗ h$ that satisfies certain conditions:
•(closed) $g ∗ h \in G$. We say that $G$ is closed under $∗$
•(associative) $g ∗ (h ∗ k) = (g ∗ h) ∗ k$ for all $g, h, k \in G$. We say that $∗$ is associative.
•(identity) There exists an identity element $d \in G$ such that for all $g \in G$
$$d ∗ g = g ∗ d = g$$
•(inverse) Every element $g \in G$ has an inverse $g^{-1}$ such that:
$$g * g^{-1}=d$$
Terminology
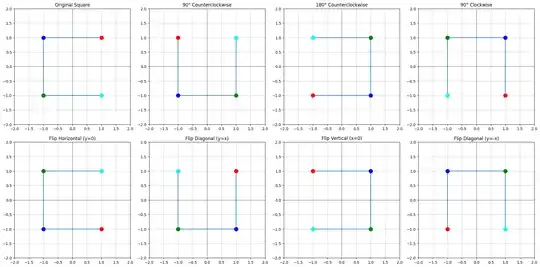
I understand this as the most abstract way to study symmetry. For example thinking on the different ways a square can be rotated with different actions, and recognizing how some combination of actions are equivalent to other simple actions.
"Roughly speaking, a symmetry of an object is a bijection (i.e. one-to-one correspondence) from the object to itself that preserves its structure." https://www.maths.gla.ac.uk/~mwemyss/teaching/3alg1-7.pdf
For example thinking about what are all the "actions" we can take on a square that leave it in an indistinguishable state from the state you started allows you to understand the 8 symmetries in the "Dihedral Group of order 8"
Each action is called a symmetry of the square (in this case we have eight):
| binary | Decimal | Action | Expression |
|---|---|---|---|
| 000 | 0 | Doing nothing | $z \mapsto z e^{2\pi i}=1z$ |
| 001 | 1 | Rotation Counterclockwise 90º | $z \mapsto z e^{\frac{i\pi}{2}}=iz$ |
| 010 | 2 | 180º rotation (can be done clockwise or anticlockwise) | $z \mapsto z e^{i\pi}=-z$ |
| 011 | 3 | Clockwise 90º rotation | $z \mapsto z e^{-\frac{i\pi}{2}}=-iz$ |
| 100 | 4 | Flipping along horizontal $y=0$ axis | $z \mapsto \overline{z}$ |
| 101 | 5 | Flipping along diagonal $y=x$ axis | $z \mapsto \overline{z}e^{\frac{i\pi}{2}} $ |
| 110 | 6 | Flipping along vertical $x=0$ axis | $z \mapsto -\overline{z}$ |
| 111 | 7 | Flipping along diagonal $y=-x$ axis | $z \mapsto -\overline{z}e^{\frac{i\pi}{2}} $ |
In these expressions, $z$ is a complex number and $\overline{z}$ represents its complex conjugate. This is a way to express these actions with an operation with complex numbers.