Main string description
To keep the core of the question short, I leave the context introduction at the end of this text. Here I describe a construction that is related to that introduction, but to answer the question you could just start reading from here.
Given N colored dots describing a curve in space $\vec{\mathbf{X_n}}$ , created by a single array of complex numbers $Z_n$ created recursively.
$$\vec{\mathbf{X_n}}=(u_n,v_n,w_n)$$
Considering: $$n \in \space \mathbb{N}_0$$
$$T_o \in \space \mathbb{Q}$$
We have
$$ r_k= \begin{cases} 0 & k < 0 \\ r_{k-1}+\Delta r_o & \space k \geq 0 \text{ and } k \equiv 0 \pmod{M} \\ r_{k-1} & \space k > 0 \text{ and } k \not\equiv 0 \pmod{M} \end{cases} $$ $$k \in \space \mathbb{Z}$$
So :
$$\omega=e^{\frac{2\pi i}{T_o}}$$
$$Z_n=r_n\omega^n$$
Coloring
The color $C_n$ in these examples is based on "hsv" or "coolwarm" colormaps with $M_c$ colors:
$$C_n \equiv n \pmod{M_{c}}$$
Coordinates
And cartesian coordinates for the sequences describing a curve in space: $$\vec{\mathbf{X_n}}=(u_n,v_n,w_n)$$
$$\Omega_o=\frac{2\pi }{T_o}$$
And the spatial coordinates arrays for index $n$
$$u_n=\frac{1}{2}(Z_n+\overline{Z_n})=r_n cos[\Omega_o n]$$
$$v_n=\frac{1}{2i}(Z_n-\overline{Z_n})=r_n sin[\Omega_o n]$$
$$w_n=log_{2}(|Z_n|)$$
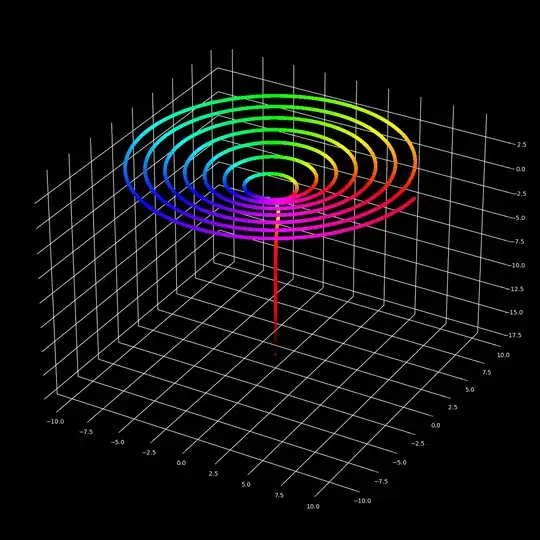
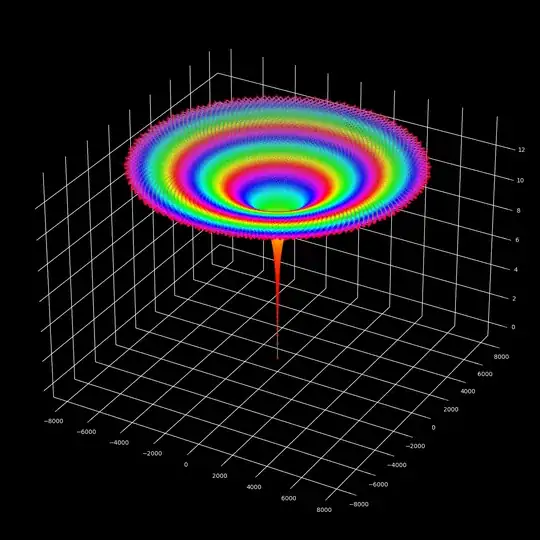
Examples with just one curve in space where periodicity is shown by the color of the scatter plot
The gray colored lines are the line between two consecutive dots.
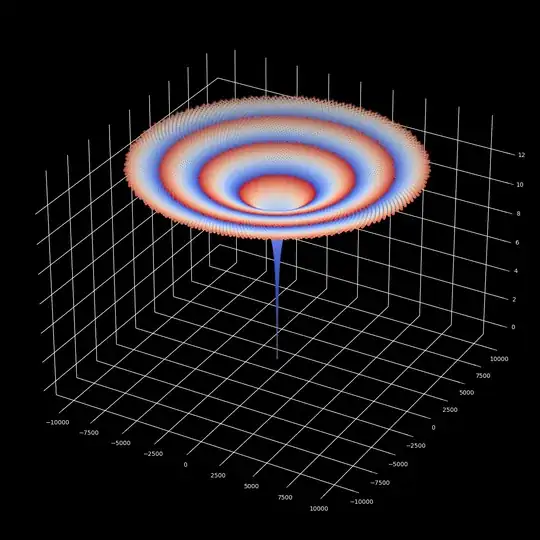
$M=13$ $M_c=13$ $T_o=13$
Because of the properties of the roots of unity, for rational $T_o$ we will always have periodicity in $\omega^n$
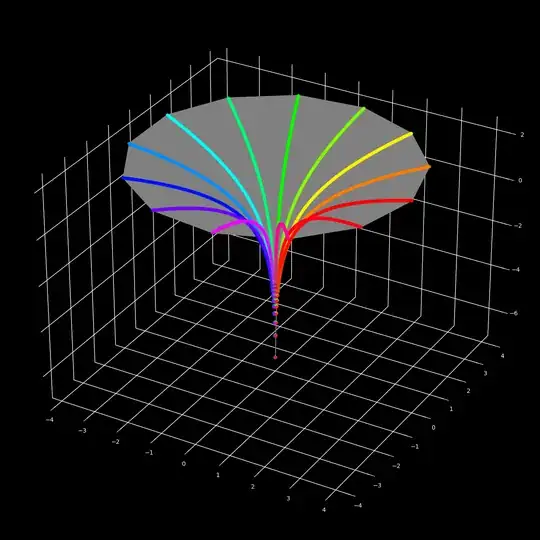
$M=1$ $M_c=13$ $T_o=13$
$M=1$ $T_o=M_c=3$
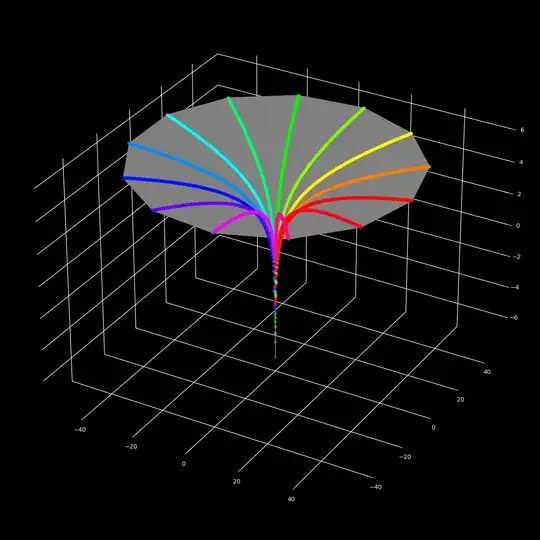
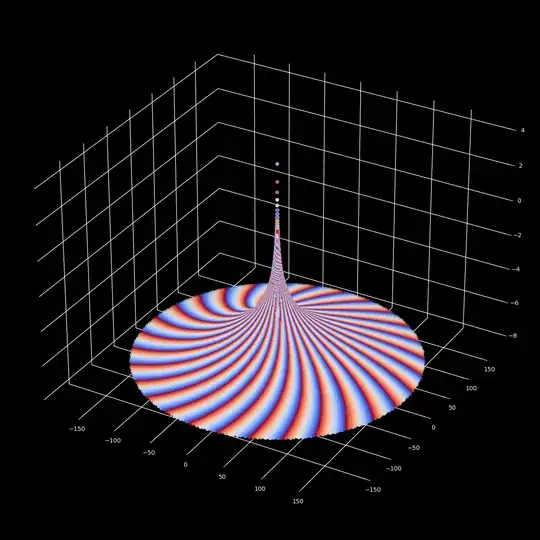
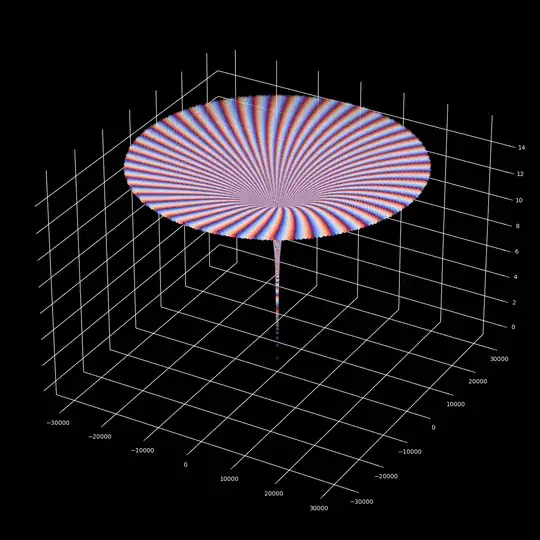
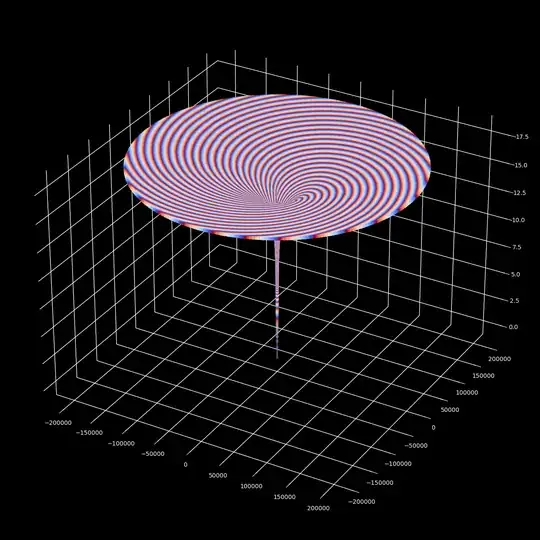
$M=1$ with big $T_o=M_c=10^5$
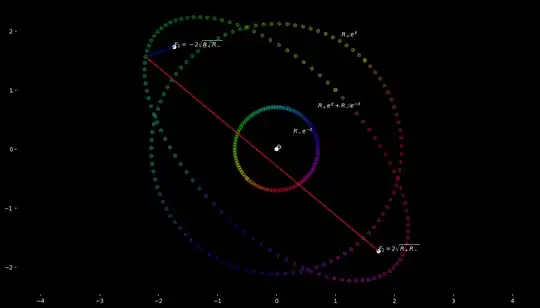
Question: What about irrational $T_o=\varphi$ corresponding to an integer $M_c$ providing some sense of "irrational-periodicity"
$$\varphi=\frac{1}{2}(1+\sqrt{5})$$
It is well known that, When dealing with "discrete-time" sequences, if $T_o$ is an irrational number, the traditional sense of periodicity fails, so $f[n+P] \neq f[n]$
$$\omega^{n}\omega^{P}\neq\omega^{n}$$
$$\omega=e^{\frac{2\pi i}{T_o}}$$
$$P \in \mathbb{N}$$
But clearly there is some periodicity in an extended sense, that can be seen in this graphs. I'd like to know how is this kind of periodicity properly described in math.
In this plots we use a rational approximations of an irrational number, what delivers a drifting effect that is very convenient to describe a predictable pattern that is not periodic in the traditional sense, and that appears to use the space more efficiently.
$M_c=M=13$ $T_o=\varphi$
Other irrational example $T_o=\sqrt{2}$ and $M_c=16$
Introduction at the end, The order matters : Math, Rhythm, Counting, Monads, Particles, Universe
Disclaimer: This is a recreational math question from a math hobbyist looking for guidance
This is TLDR introduction for the question, but the reason is to give context of why I'm looking for guidance and good reads on how to describe some mathematical definitions as periodicity in an extended sense.
I left this at the end so the important part of the question is at the top.
I saw a post in X that said:
"Numbers are particles"
I immediately thought I agree, without even understanding clearly the meaning in the real world of such a statement. just thought in my infinite ignorance, I agree. That sounds nice.
That's what I've been thinking about monads, trying to understand how just the process of evolving-time could be enough to create geometry and this way creating everything that is observable, expanding from an initial spatial and temporal coordinate and evolving according to a simple set of initial rules.
Math is the best infinite game available for humans (not only mathematicians), and I had the "irrational" impulse of start working on a model of a toy-universe where math is creating everything using the energy and information associated to the beat of a "drum" or the tick of a "clock" at the center of coordinates, what in our game would be "the center of the universe".
So we can think of a model of a toy-universe using a set of initial conditions and simple set of rules that ends up describing a set of orbi-curves able to describe some fundamental geometric shapes flexible enough to create everything else, all monads information being governed by local phenomena and the timing and syncing governed by a binary clock at the center of the universe.
¿How does a mathematician think about designing/describing ad-hoc bridges between binary counting, geometric shapes, monads, vectors using complex numbers?
I know many of the relations described here are well known, and that periodicity has enhanced meanings in different contexts, but I'd love some one to point me to some reading discussing these kind of constructions.
About why choosing the word Monad for the toy-universe game
We can think of a monad as a virtual particle, that is able to "reflect" or "refract" some information with it's own essential bias, a feature that can be seen as a color or an associated symbol .
Another way we can imagine a monad for our experiment is as a musical note able to create in connection with others a geometry that is predictable by our brains, making it more enjoyable.
When I think of monads I think about an "a-priori-random" set of events that leave as a trace of their occurrence a set of "a-priori-indivisible" entities that have some information associated to them, and this information can be thought as a biased-reflection of their immediate context and the whole system state, but at the same time these entities have their own essence given by the "universe-architect" at the "beginning", being able to position the monad in context with others, in a specific spatial and temporal coordinate, working as some kind of universe-building-celular-automata governed by the simplest central rules (Central binary clock or "Drum").
But using Wikipedia we see some of the real meanings of the word:
In philosophy: An ultimate atom, or simple, unextended point; something ultimate and indivisible.
In functional programming: A data type which represents a specific form of computation, along with the operations "return" and "bind".
In category theory: A monoid object in the category of endo-functors of a fixed category. ¿¿¿What???
Co-monad as a monad of the opposite category. This makes me think for example "monads" 1 with -1 as the main items in the category positive and negative integers, but also as a sense of direction in space like spin.
For context we should mention Leibniz's "La Monadologie"
Leibniz surmised that there are indefinitely many substances individually 'programmed' to act in a predetermined way, each substance being coordinated with all the others.
This is the pre-established harmony which solved the mind-body problem, but at the cost of declaring any interaction between substances a mere appearance.
The clock at the center of the universe
We can imagine a tick of a clock in the center of the toy-universe, that is there from the beginning. Each tick is transmitted to the whole universe through a time-wave that travels "instantaneously" everywhere bringing motion to everything that is being built since the "Big Drum Celular Automata Process" started.
Why binary counting
We can imagine each monad in the system as being created and transformed by every tick of the clock. This can be thought as some kind of universal digital circuit, where a main clock syncs everything with everything else. In this toy-universe-game the idea is to allow this central clock to provide a geometry where "reality" is displayed.
Binary counting and coordinate shifting of a curve in space
Given N "monads" describing a curve in space $\vec{\mathbf{X_n}}$ , created by a single array of complex numbers $Z_n$
$$\vec{\mathbf{X_n}}=(u_n,v_n,w_n)$$
Considering: $$n \in \space \mathbb{N}_0$$
$$T_o \in \space \mathbb{R}$$
We have
$$\omega=e^{\frac{2\pi i}{T_o}}$$
And
$$Z_n=r_n\omega^n$$
$$\overline{Z_n}=r_n\omega^{-n}$$
The modulus of $Z_n$ can have many growth rules, for the initial set of examples we will use the following recursive rules to keep things simple:
$$|Z_n|=r_n$$
Coloring
The color $C_n$ in these examples is based on "hsv" or "coolwarm" colormaps with $M_c$ colors:
$$C_n \equiv n \pmod{M_{c}}$$
Designing the modulus of $Z_n$ recursively
For a given positive integer $M$, as the maximum amount of monads allowed per same-radius-circumference, and a real number $\Delta r_o$ defining in this case the discrete growth of r_n every time $n \equiv 0 \pmod{M}$.
$$ r_k= \begin{cases} 0 & k < 0 \\ r_{k-1}+\Delta r_o & \space k \geq 0 \text{ and } k \equiv 0 \pmod{M} \\ r_{k-1} & \space k \geq 0 \text{ and } k \not\equiv 0 \pmod{M} \end{cases} $$
Considering:
$$ k \in \mathbb{Z}$$
$$ \Delta r_o \in \mathbb{R}$$
So we can imagine a "discrete-time" main index for the model of creation process in the proposed toy-universe:
$$n=[0,1,2,3,4,...,N-1]$$
We define the main set of arrays describing a curve in space
$$\vec{\mathbf{X_n}}=(u_n,v_n,w_n)$$
$$\Omega_o=\frac{2\pi }{T_o}$$
And the spatial coordinates arrays for index $n$
$$u_n=\frac{1}{2}(Z_n+\overline{Z_n})=r_n cos[\Omega_o n]$$
$$v_n=\frac{1}{2i}(Z_n-\overline{Z_n})=r_n sin[\Omega_o n]$$
$$w_n=\frac{log(|Z_n|)}{log(2)}$$
So we have an analogous way to see that:
$$Z_n=u_n+iv_n$$
$$\overline{Z_n}=u_n-iv_n$$
So from a simple 2D numbers array $Z_n$, we can construct 8 curves in space , given by the $2^{3}$ symmetries in the positive $w$ direction
Consider:
$$R_n=\frac{v_n}{u_n}$$
$$\vec{\mathbf{V_n}}=(k_u u_n,k_v v_n,k_w w_n)$$
- xyz x4 - Four basic symmetries for a complex number
| Binary | Decimal | Curve | LSb Symmetry | $k_u$ | $k_v$ | $k_w$ |
|---|---|---|---|---|---|---|
| 000 | 0 | A | $u_n+ iv_n$ | 1 | 1 | 1 |
| 001 | 1 | B | $u_n- iv_n$ | 1 | -1 | 1 |
| 010 | 2 | C | $-u_n+ iv_n$ | -1 | 1 | 1 |
| 011 | 3 | D | $-u_n- iv_n$ | -1 | - 1 | 1 |
- yxz x4 - Four basic symmetries for a coordinate shift on a complex number
| Binary | Decimal | Curve | LSb Symmetry | $k_u$ | $k_v$ | $k_w$ |
|---|---|---|---|---|---|---|
| 100 | 4 | E | $v_n +iu_n$ | $R_n$ | $\frac{1}{R_n}$ | 1 |
| 101 | 5 | F | $v_n -iu_n$ | $R_n$ | $-\frac{1}{R_n}$ | 1 |
| 110 | 6 | G | $-v_n +iu_n$ | $-R_n$ | $\frac{1}{R_n}$ | 1 |
| 111 | 7 | H | $-v_n -iu_n$ | $-R_n$ | $-\frac{1}{R_n}$ | 1 |
We could continue this table for $k_w=-1$, with the mirrored curves totaling $2^4$ mirrored curves
This change is iust to indicate more clearly that up to 48 curves can be created mirroring the same $\vec{X}$, being the first 8 paths:
$$\vec{X_n}=(k_u u_n,k_v v_n,k_w w_n)$$
For example an array describing a set of curves we will call "Flower" uses 8 mirrored arrays :
- xyz x4
$$\vec{A_n}=(u_n,v_n,w_n)$$ $$\vec{B_n}=(u_n,-v_n,w_n)$$ $$\vec{C_n}=(-u_n,v_n,w_n)$$ $$\vec{D_n}=(-u_n,-v_n,w_n)$$
- yxz x4
$$\vec{E_n}=(v_n,u_n,w_n)$$ $$\vec{F_n}=(v_n,-u_n,w_n)$$ $$\vec{G_n}=(-v_n,u_n,w_n)$$ $$\vec{H_n}=(-v_n,-u_n,w_n)$$
Other alphabets describing mirrored set of curves
Following the previous logic, we can imagine:
"Wormhole" structure created by counting
"Wormhole" using 16 Mirrored curves :
- xyz x4
$$\vec{A_n}=(u_n,v_n,w_n)$$
$$\vec{B_n}=(u_n,-v_n,w_n)$$
$$\vec{C_n}=(-u_n,v_n,w_n)$$
$$\vec{D_n}=(-u_n,-v_n,w_n)$$
- yxz x4
$$\vec{E_n}=(v_n,u_n,w_n)$$
$$\vec{F_n}=(v_n,-u_n,w_n)$$
$$\vec{G_n}=(-v_n,u_n,w_n)$$
$$\vec{H_n}=(-v_n,-u_n,w_n)$$
- xy(-z) x4 $$\vec{I_n}=(u_n,v_n,-w_n)$$
$$\vec{J_n}=(u_n,-v_n,-w_n)$$
$$\vec{K_n}=(-u_n,v_n,-w_n)$$
$$\vec{L_n}=(-u_n,-v_n,-w_n)$$
- yx(-z) x4 $$\vec{M_n}=(v_n,u_n,-w_n)$$
$$\vec{N_n}=(v_n,-u_n,-w_n)$$
$$\vec{O_n}=(-v_n,u_n,-w_n)$$
$$\vec{P_n}=(-v_n,-u_n,-w_n)$$
"Atomic" structure created by counting
"Atom" structure uses 6*8=48 curves using all possible basic-combinations of shifted coordinates :
$F_0$
- xyz x4
$$\vec{A_n}=(u_n,v_n,w_n)$$
$$\vec{B_n}=(u_n,-v_n,w_n)$$
$$\vec{C_n}=(-u_n,v_n,w_n)$$
$$\vec{D_n}=(-u_n,-v_n,w_n)$$
- yxz x4
$$\vec{E_n}=(v_n,u_n,w_n)$$
$$\vec{F_n}=(v_n,-u_n,w_n)$$
$$\vec{G_n}=(-v_n,u_n,w_n)$$
$$\vec{H_n}=(-v_n,-u_n,w_n)$$
$F_1$
- xy(-z) x4 $$\vec{I_n}=(u_n,v_n,w_n)$$
$$\vec{i_n}=(u_n,-v_n,-w_n)$$
$$\vec{K_n}=(-u_n,v_n,-w_n)$$
$$\vec{L_n}=(-u_n,-v_n,-w_n)$$
- yx(-z) x4 $$\vec{M_n}=(v_n,u_n,-w_n)$$
$$\vec{N_n}=(v_n,-u_n,-w_n)$$
$$\vec{O_n}=(-v_n,u_n,-w_n)$$
$$\vec{P_n}=(-v_n,-u_n,-w_n)$$
$F_2$
- zxy x4
$$\vec{Q_n}=(w_n,u_n,v_n)$$
$$\vec{R_n}=(w_n,u_n,-v_n)$$
$$\vec{S_n}=(w_n,-u_n,v_n)$$
$$\vec{T_n}=(w_n,-u_n,-v_n)$$
- zyx x4
$$\vec{U_n}=(w_n,v_n,u_n)$$
$$\vec{V_n}=(w_n,v_n,-u_n)$$
$$\vec{W_n}=(w_n,-v_n,u_n)$$
$$\vec{X_n}=(w_n,-v_n,-u_n)$$
$F_3$
- (-z)xy x4
$$\vec{\alpha_n}=(-w_n,u_n,v_n)$$
$$\vec{\beta_n}=(-w_n,u_n,-v_n)$$
$$\vec{\gamma_n}=(-w_n,-u_n,v_n)$$
$$\vec{\delta_n}=(-w_n,-u_n,-v_n)$$
- (-z)yx x4
$$\vec{\epsilon_n}=(-w_n,v_n,u_n)$$
$$\vec{\zeta_n}=(-w_n,v_n,-u_n)$$
$$\vec{\eta_n}=(-w_n,-v_n,u_n)$$
$$\vec{\theta_n}=(-w_n,-v_n,-u_n)$$
$F_4$
- xzy x4
$$\vec{\iota_n}=(u_n,w_n,v_n)$$
$$\vec{\kappa_n}=(u_n,w_n,-v_n)$$
$$\vec{\lambda_n}=(-u_n,w_n,v_n)$$
$$\vec{\mu_n}=(-u_n,w_n,-v_n)$$
- yzx x4
$$\vec{\nu_n}=(v_n,w_n,u_n)$$
$$\vec{\xi_n}=(v_n,w_n,-u_n)$$
$$\vec{O_n}=(-v_n,w_n,u_n)$$
$$\vec{\pi_n}=(-v_n,w_n,-u_n)$$
$F_5$
- x(-z)y x4
$$\vec{\rho_n}=(u_n,-w_n,v_n)$$
$$\vec{\sigma_n}=(u_n,-w_n,-v_n)$$
$$\vec{\tau_n}=(-u_n,-w_n,v_n)$$
$$\vec{\upsilon_n}=(-u_n,-w_n,-v_n)$$
- y(-z)x x4
$$\vec{\phi_n}=(v_n,-w_n,u_n)$$
$$\vec{\chi_n}=(v_n,-w_n,-u_n)$$
$$\vec{\psi_n}=(-v_n,-w_n,u_n)$$
$$\vec{\omega_n}=(-v_n,-w_n,-u_n)$$
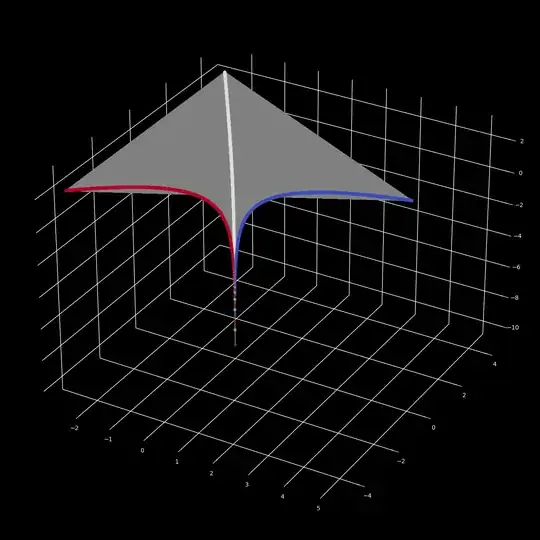
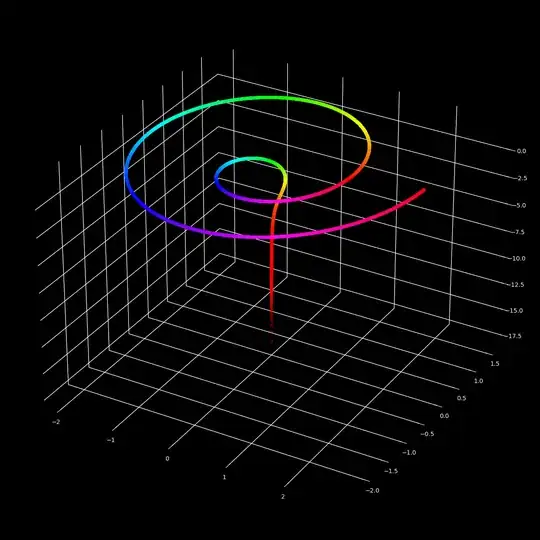




@replieswork? I saw your comment because I'm specifically following the question, but to ensure a user gets a notification that you've responded, don't forget to use the@feature and the autocomplete. As for your comment - are you sure the question is currently clear enough and can be answered directly, rather than just a "here's what I'm thinking about" announcement? – uhoh Jun 10 '24 at 22:42