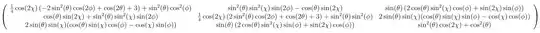Decompose a $3 \times 3$ orthogonal matrix into a product of rotation and reflection matrices

Question

It holds that every orthogonal matrix can be expressed as a product of rotation and reflection matrices.

We can prove that every $2 \times 2$ orthogonal matrix can be represented in the form

$$\begin{bmatrix}\cos\theta&\mp\sin\theta\\\sin\theta&\pm\cos\theta\end{bmatrix}$$

Similarly, can we find a general decomposition of a $3 \times 3$ orthogonal matrix into rotation and reflection matrices? In other words, I would like a general decomposition or algorithm to be able to fill in the blanks for any $3 \times 3$ orthogonal matrix in the following statement: "This matrix represents a rotation by _____ followed by a reflection along _____".

I tried to use the property $Q^TQ = I$ for an orthogonal matrix $$Q = \begin{bmatrix}a&b&c\\d&e&f\\g&h&i\end{bmatrix}$$

to get $$\left\{\begin{array}{l}a^2+b^2+c^2=1\\d^2+e^2+f^2=1\\g^2+h^2 +i^2=1\\ad+be+cf=0\\ag+bh+ci=0\\ag+eh+fi=0\end{array}\right. $$

However, I'm not sure how to proceed.

Answer 1

Once the three eigenvalues $\lambda_i$ and associated eigenvectors $\vec x_i$ of $Q$ are computed, there are two complex-conjugated eigenvalues $e^{\pm i \phi}$ where $\phi$ is the rotation angle, and the real-valued eigenvalue is $\pm 1$. ($\cos\phi$ can be constructed from the trace of $Q$ without actually solving the diagonalization... see https://en.wikipedia.org/wiki/Rotation_matrix) The sign of the real-valued eigenvalue is positive if this is a pure rotation, otherwise a reflection is involved. (In fact the sign of the determinant $|Q|$ will already tell whether a reflection is invovled.) The eigendecomposition is https://en.wikipedia.org/wiki/Eigendecomposition_of_a_matrix $$ Q = M \Lambda M^{-1} $$ where $M$ contains the eigenvectors and $\Lambda$ is the diagonal matrix with the eigenvalues. The real-valued eigenvector points along the rotation axis. The aim is to decompose $Q$ as reflection and rotation matrices: $$ Q = Q^{ref} Q^{rot} $$ The rotation part is given either by $Q$ or (if reflection is involved) by flipping the signs of the components of $\vec x_i$ plus the sign of the eigenvalue in $M$ and $\Lambda$: $$ Q^{rot} = M' \Lambda' {M'}^{-1} $$ where the primes denote the entries with these potentially flipped signs, i.e., the diagonal matrix $\Lambda'$ has eigenvalues $e^{\pm i\phi}$ and $1$. (Alternatively construct $Q^{rot}$ by Mercer's theorem.) The reflection part follows from $$ Q^{ref} = Q {Q^{rot}}^{-1} $$ where ${Q^{rot}}^{-1}= {Q^{rot}}^T$, the transpose, because this is a pure rotation.

Answer 2

The answer below is based on Jyrki Lahtonen's comment, this paper on Euler angles, and these lecture notes on rotation matrices.

$\newcommand{\atant}{\text{atan2}}\newcommand{\tr}{\text{Tr }}$ If $\det(Q) = 1$, $Q$ represents a proper rotation. Hence, we can decompose $$Q = \begin{bmatrix}Q_{11}&Q_{12}&Q_{13}\\Q_{21}&Q_{22}&Q_{23}\\Q_{31}&Q_{32}&Q_{33}\end{bmatrix}=R_z(\gamma)R_y(\beta)R_x(\alpha)$$

If $Q_{31} = \pm1$, $$\alpha = \atant(-Q_{31}\cdot Q_{12}, -Q_{31}\cdot Q_{13}), \quad \beta = -Q_{31}\cdot \pi/2, \quad \gamma =0$$

Else,

$$\alpha = \atant\left(\frac{Q_{32}}{\cos(\beta)}, \frac{Q_{33}}{\cos(\beta)}\right), \quad \beta = -\arcsin(Q_{31}), \quad \gamma = \atant\left(\frac{Q_{21}}{\cos(\beta)}, \frac{Q_{11}}{\cos(\beta)}\right)$$

$\atant$ is the 2-argument arctangent function,

$$R_x(\theta) = \begin{bmatrix}1&0&0\\0&\cos(\theta)&-\sin(\theta)\\0&\sin(\theta)&\cos(\theta)\end{bmatrix}, \quad R_y(\theta) = \begin{bmatrix}\cos(\theta)&0&\sin(\theta)\\0&1&0\\-\sin(\theta)&0&\cos(\theta)\end{bmatrix}, \quad R_z(\theta) = \begin{bmatrix}\cos(\theta)&-\sin(\theta)&0\\\sin(\theta)&\cos(\theta)&0\\0&0&1\end{bmatrix}$$

If $\det(Q) = -1$, we can decompose $$Q = (QR)R, \quad R = \begin{bmatrix}1&0&0\\0&1&0\\0&0&-1\end{bmatrix}$$

We have $(QR)^T = R^TQ^T = R^{-1}Q^{-1} = (QR)^{-1}$ and $\det(QR) = \det(Q)\det(R) = -1 \cdot -1 = 1$. Hence $QR$ represents a proper rotation and can be decomposed as above. $R$ represents a reflection w.r.t the $x$-$y$ plane.

Alternatively, we have the following.

The rotation angle $\theta$, in a convention where $0\le\theta\le\pi$, is obtained from $$\cos(\theta) = \frac{1}{2}(\tr Q - \det Q),$$ and the corresponding rotation axis $\mathbf{\hat{n}}$ (which can be identified with the unit normal to the reflection plane if $\det Q = -1$) is obtained from: $$\mathbf{\hat{n}} = \frac{1}{\sqrt{(3 - \tr Q \det Q)(1 + \tr Q \det Q)}}\left(Q_{32}-Q_{23}, Q_{13} - Q_{31}, Q_{21}-Q_{12}\right),$$ for $\tr Q \det Q \neq -1, 3$.

Answer 3

An orthogonal matrix consists of pairwise orthogonal rows and columns. So they form an orthogonal basis as images of the unit vectors which fall in two categories, volume form $\pm 1$, its coefficent is the determinant, that counts reflections in the basis mod 2.

Correcting the determinant to 1 by multiplying the matrix with a unit matrix with one entry changed to $-1$ with the effect, that a row from left or a column from right changes sign.

By Eulers theorem in three dimensions, a proper rotation is a rotation by an angle $\chi$ around a unit vector in spherical coordinates on the upper semi-sphere is $$\vec n =\left(\sin\theta \cos\phi ,\ \ \sin\theta \sin\phi,\ \ \cos \theta \right), \quad 0 \ < \ \theta \ < \ \frac{\pi}{2}, \quad 0<\phi<2\pi.$$ The angle of rotation in the 1-2-plane $$A=\left( \begin{array}{ccc} \cos \chi & -\sin \chi & 0\\ \sin \chi & \cos \chi & 0 \\ 0 & 0 & 1 \end{array}\right)$$ obviously is given by the trace $$1+2 \ \cos \chi = \text{Tr}( A) $$ Trace and determinant as commutative maps involving sum and products of eigenvalues only, are invariant under rotations.

It's possible now, to determine the two angles of the rotation axis by taking traces with the Lie-basis

$$\left( L_i\right)_{\alpha \beta}=\delta_{i\alpha} - \delta_{i\beta}$$

$$L=\left\{\text{L1}\ = \ \left( \begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & -1 \\ 0 & 1 & 0 \\ \end{array} \right),\quad \text{L2} \ = \ \left( \begin{array}{ccc} 0 & 0 & 1 \\ 0 & 0 & 0 \\ -1 & 0 & 0 \\ \end{array} \right),\quad \text{L3}\ = \ \left( \begin{array}{ccc} 0 & -1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \\ \end{array} \right)\right\}$$

A rotation matrix with the 3-axis is the matrix exponential

$$\text{SO3}(\chi,\ (0,0,1)) = e^{\chi \ L3}= Id_3 \ + \ (\cos\chi -1) \ L_3^2 \ + \ L3 \ \sin\chi \ = \ A $$

We conclude from spherical symmetry that the general rotation matrix is the exponential of the linear combination of the 3 generators with the components of axis vector by the general commutativity of powers and roations and there for with functions

$$O_3 f( x ) O^{-1} = f(O_3 x \ \ O^{-1}) \quad \text {by} \ O x x O^{-1}=O x O O^{-1} x O{-1}= (O x O^{-1}) ^2$$

we can construct the rotation matrix in $SO(3)$ by the exponential of of the generators, the three antisymmetric unit matrices

$$\text{SO}_3\left(\chi ,\ (\theta \,\phi )\right)=e^{\chi\ * (\text{L1} \ \sin (\theta ) \ \cos (\phi )\ + \ \text{L2} \ \sin (\theta ) \ \sin (\phi ) \ + \ \text{L3} \ \cos (\theta ))}$$

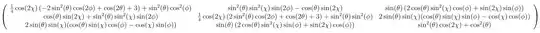
The angle of rotation and the polar angles of the rotation axis can be retrieved via the linear form of taking the trace of products with the basis of Lie-matrix algebra. Using Mathematica, the eigenvalues are

   Eigensystem[Subscript[SO, 3][\[Chi], {\[Theta], \[Phi]}]][[1]]

$$\left\{1,e^{-2 i \chi },e^{2 i \chi }\right\}$$

and as a check the first eigenvector corresponding to the eigenvalue 1

  Eigensystem[Subscript[SO, 3][\[Chi], {\[Theta],\[Phi]}]][[2,1]] 

$$\{\tan (\theta ) \ \cos (\phi ),\ \tan (\theta ) \ \sin (\phi ), \ 1\}$$

The traces with the Lie-basis yields

$$\begin{align} &\text{Tr}\left[\text{SO}_3(\chi ,\{\theta ,\phi \})\right] \ = \ -2 \ \cos (2 \chi )+1 \\ &\text{Tr}\left[\text{L1}.\text{SO}_3(\chi ,\{\theta ,\phi \})\right] \ = \ -2 \ \sin (\theta ) \sin (2 \chi ) \ \cos (\phi ) \\ & \text{Tr}\left[\text{L2}.\text{SO}_3(\chi ,\{\theta ,\phi \})\right] \ = \ -2 \ \sin (\theta ) \sin (2 \chi ) \ \sin (\phi ) \\ &\text{Tr}\left[\text{L3}.\text{SO}_3(\chi ,\{\theta ,\phi \})\right] \ = \ -2 \ \cos (\theta ) \ \sin (2 \chi ) \\ \end{align}$$

By the usual trigonmetrics

$$\begin{align} &\cos \chi \ = \ \frac{1}{2}\ (\text{Tr}[O]-1) \\ &\sin^2 \chi \ =1-\frac{1}{4} (\text{Tr}[O]-1)^2 \\ &\tan \phi \ = \ \frac{\text{tr}_2}{\text{tr}_1} \\ &\sin^2 \theta \ = \ \frac{\text{tr}_2^2+\text{tr}_3^2}{4-(\text{Tr}(O)-1)^2} \\ \end{align}$$