4

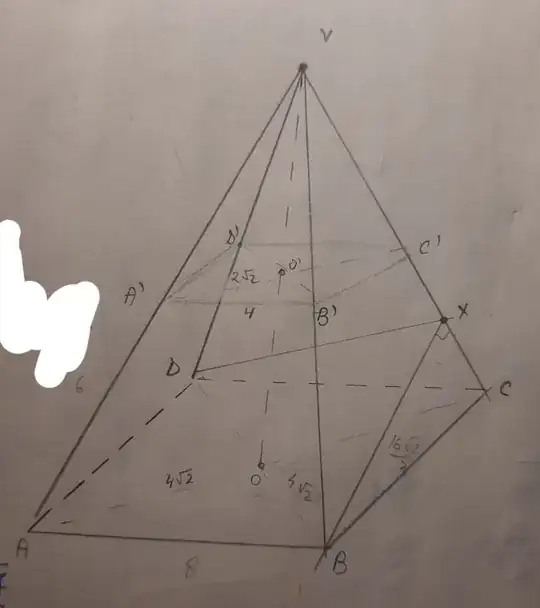
The problem

Let the trunk be a regular quadrilateral pyramid $ABCDA'B'C'D'$ with the side of the large base of $8$ cm and the side of the small base of $4$ cm. The lateral faces are isosceles trapezoids that can be circumscribed in a circle.

$a)$ Determine the lateral area and the volume of the pyramid trunk

$b)$ Calculate the sine of the angle of two side faces of the trunk

My solution

Drawing

enter image description here

$a)$ As you can see I drew the whole pyramid including its peak $V$.

Because the lateral faces are isosceles trapezoids that can be circumscribed in a circle we get that $AA'=\frac{B+b}{2}=6$ cm

Then he can calculate the height of the trapezoids $h=4\sqrt{2}$

In the right angled trapezoid $A'O'OA$ we can calculate $OO'=2\sqrt {7}$

Now we have everything to calculate the lateral area and the volume of the trunk

$A_l= \frac{(P_B+P_b)*h}{2}=\frac{48*4*\sqrt{2}}{2}= 96\sqrt{2}$

$V= \frac{h}{3}*(A_B+A_b+\sqrt{A_b+A_B})=\frac{2\sqrt{7}*112}{3}=\frac{224\sqrt{7}}{3}$

For point $b)$ we have to find the sine of the angle between $(VBC)$ and $(VDC)$

I let $BX \perp VC$ and by the congruence of the triangles $DXC$ and $BXC$ we get that $DX \perp VC$ so the angle we look for is $\angle DXC$

Triangle is isosceles with $DX=BX=\frac{16\sqrt{2}}{3}$ and $DB=8\sqrt{2}$ so $OX=\frac{4\sqrt{14}}{3}$ so we can express the area of triangle $DXB$ in $2$ ways the find the sin of that angle and I get that $sin= \frac{3\sqrt{7}}{8}$

I put this as a solution verification because I'm not sure if this part is right, Because the lateral faces are isosceles trapezoids that can be circumscribed in a circle we get that $AA'=\frac{B+b}{2}=6$ cm".

Also, I'm not sure if my calculus and idea for point $b)$ are right

I hope one of you can help me! Thank you!

IONELA BUCIU
  • 673
  • 1
    Enough with the trivial edits, already. – Gerry Myerson Jul 08 '24 at 12:55
  • 1
    Your answers for the lateral area and the sine of the angle are correct. Good work. (+1) –  Jul 08 '24 at 14:31
  • @mathlove What is the info you are talking about? I used the fact that the trapezoids can be circumscribed – IONELA BUCIU Jul 08 '24 at 16:55
  • @mathlove Oo.... i thought it the wrong way, tho corect me if I'm wrong, but in the 2nd source, it says that the quadrilateral is circumscribed. – IONELA BUCIU Jul 09 '24 at 11:33
  • @mathlove This is what i was reffering to : ,, Since these quadrilaterals can be drawn surrounding or circumscribing their incircles, they have also been called circumscribable quadrilaterals, circumscribing quadrilaterals, and circumscriptible quadrilaterals." – IONELA BUCIU Jul 09 '24 at 12:06
  • It does not say "the quadrilateral is circumscribed". You might want to check the meaning of the word "circumscribe". (1) "A circumscribes B" basically means "B is in A" (see the first sentence of this question and the drawing in its answer). (2) "A is circumscribed in B" basically means "A is in B" (see the first sentence in this question) – mathlove Jul 09 '24 at 12:37
  • @mathlove Oooo...thanks! Now i understand! But how should I solve it then? is there a thing that any trapezoids that are issoscels and can be circumscribed can also be inscribed or any formula? – IONELA BUCIU Jul 09 '24 at 13:53
  • The official name for that shape is a pyramidal frustum. – Nate Jul 10 '24 at 01:49
  • The official name of OPs.quad. is tangential quadrilateral. – Bob Dobbs Jul 10 '24 at 07:35

2 Answers2

1

Point $a)$ is correct. Since we are given that a circle is inscribable in the isosceles trapezoid, we know from the tangency that$$AA’=\frac{AB}{2}+\frac{A’B’}{2}=4+2=6$$and from this the lateral area and volume are as OP calculates.

Point $b)$ is also correct: since$$\sin\angle OXB=\frac{BO}{BX}=\frac{4\sqrt 2}{\frac{16\sqrt 2}{3}}=\frac{3}{4}$$and$$\cos\angle OXB=\frac{OX}{BX}=\frac{\frac{4\sqrt {14}}{3}}{\frac{16\sqrt 2}{3}}=\frac{\sqrt 7}{4}$$and$$\angle DXB=2\angle OXB$$and$$\sin2\theta=2\sin\theta\cos\theta$$then$$\sin\angle DXB=2\cdot\frac{3}{4}\cdot \frac{\sqrt7}{4}=\frac{3\sqrt 7}{8}$$

Edward Porcella
  • 5,178
  • Thanks for you answer! So the discussion in the comments isn't right, because still cant make the difference between source 1 and 2? – IONELA BUCIU Jul 10 '24 at 10:47
  • 1
    Every isosceles trapezoid has a circumcircle, but here you have one that has an incircle too. This enables you to say (because of tangency) that $AA’=6$. I think your second sentence should be “Because the lateral faces are isosceles trapezoids that circumscribe a circle….” – Edward Porcella Jul 10 '24 at 13:04
0

Your numerical results are correct.

In point a, the volume formula is

$$V=\frac{2h}{3}A_B-\frac h3 A_b.$$

In point b, you could also find $\sin\theta$, $\theta=\angle DXB$, by using the formula $$\cos\theta=-\cot^2\alpha$$ where $\alpha$ is the base angle of the trapezoids.
$$\cot\alpha=\frac4{8\sqrt2}=\frac1{2\sqrt2}$$ hence $\cos\theta=-\frac18$, $\sin\theta=\frac{3\sqrt7}8.$

Bob Dobbs
  • 15,712