The problem goes like this-
A chemical process is used to remove impurities from a pulp by bleaching process generating toxic and non-toxic wastes.
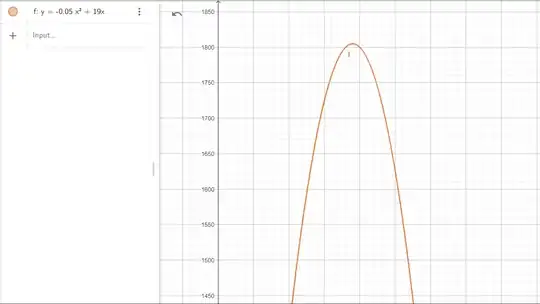
The toxic waste generated is 0.05 times the square of the amount of chemical used, while the non-toxic waste generated is 0.1 times the amount of chemical used. The pulp yield is 19.1 times the amount of chemical used.
Determine the amount of chemical to be used to maximize the pulp yield and minimize the waste?
My approach is trying to form single variable functions for the total waste & yield. Then take the ratio of yield and total waste and try to maximize it. The derivative is coming out to be decreasing function with value tending to infinity at the boundry (chemical used=0). I am stuck at this limbo.
Any improvement of this process or new approach would be of great help to me