Unions & Intersection of Probability

Question

I've had all three answers below marked wrong, and I am not sure how to proceed. I have included my thinking.

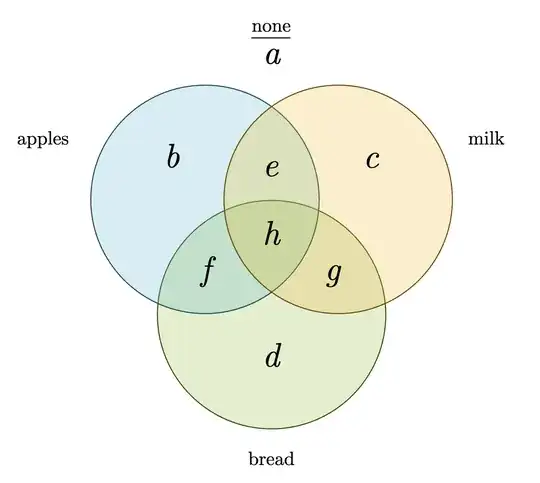
Suppose we are interested in the buying habits of shoppers at a particular grocery store with regards to whether they purchase apples, milk, and/or bread. Now suppose $30\%$ of all shoppers at this particular grocery store buy apples, $45\%$ buy milk, and $40\%$ buy a loaf of bread.
Let $A$ be the event that a randomly selected shopper buys apples, $B$ be the event that the same randomly selected shopper buys milk, and $C$ the event that the shopper buys bread. Suppose we also know (from data collected) the following information:

• The probability that the shopper buys apples and milk is $0.20$.
• The probability that the shopper buys milk and bread is $0.25$.
• The probability that the shopper buys apples and bread is $0.12$.
• The probability that the shopper buys all three items is $0.07$.

a) Find the probability that the shopper purchases at least one of the three items.

My attempt :
$P(A \cup B \cup C) = P(A)+P(B)+P(C)-P(A \cap B)-P(B \cap C)-P(A \cap C)+P(A \cap B \cap C)=.30+.45+.40-.2-.25-.12 + .17 =0.75$

b) Find the probability that the shopper purchases none of the three items.

My attempt :
$P(A' \cup B' \cup C')=(1-.3) \times (1-.45) \times (1-.4)=.7 \times .45 \times .4 = .231$

c) Find the probability that the shopper buys milk and bread but not apples.

My attempt :
$P(A' \cap B \cap C)=(1-.3) \times .45 \times .4 =0.126$

EDIT

I have also tried doing this with naive probability and the answers are still not accepted.

a)
s=c(111, 110, 101, 011, 100, 001, 010, 000)
s_count=8
at_least_1= c(111, 110, 101, 011, 100, 001, 010)
at_least_1_ct=7
7/8=0.875

b)
none=c(111, 110, 101, 011, 100, 001, 010, 000)
1/8=0.125

c)
milk_and_bread=c(111, 110, 101, 011, 100, 001, 010, 000)
2/8=0.25

Answer 1

c) Find the probability that the shopper buys milk and bread but not apples.

My attempt: $P(A' \cap B \cap C)=(1-.3) \times .45 \times .4=0.126$

$$P(A' \cap B \cap C)=\mathbf{0.18}\ne0.126= P(A')\times P(B)\times P(C).$$ (The correct answer $\mathbf{0.18}$ is explained below.) Thus, events $A',B,C$ are not in fact mutually independent. So, events $A,B,C$ are also not independent.

Incidentally, note that

• $P(X \cap Y \cap Z)=P(X)\times P(Y)\times P(Z){\kern.6em\not\kern-.6em\implies}$ $X,Y,Z$ are independent
• $X,Y,Z$ are pairwise independent ${\kern.6em\not\kern-.6em\implies} P(X \cap Y \cap Z)=P(X)\times P(Y)\times P(Z).$

b) Find the probability that the shopper purchases none of the three items.

My attempt: $P(A' \cup B' \cup C')=(1-.3) \times (1-.45) \times (1-.4)=.231$

You meant to write $P(A' \cap B' \cap C');$ unfortunately, as above, $$P(A' \cap B' \cap C')\ne P(A')\times P(B')\times P(C').$$

a) Find the probability that the shopper purchases at least one of the three items.

My attempt: $P(A \cup B \cup C) = P(A)+P(B)+P(C)-P(A \cap B)-P(B \cap C)-P(A \cap C)+P(A \cap B \cap C)=.30+.45+.40-.2-.25-.12 + .17 =0.75$

You misread $0.07$ as $0.17,$ so your answer is too big by $0.10.$

---

A CORRECT SOLUTION

Let $A$ be the event that a randomly selected shopper buys apples, $B$ be the event that the same randomly selected shopper buys milk, and $C$ the event that the shopper buys bread.

Why does the problem statement make $B$ stand for Milk instead of Bread? To lower the cognitive load, thereby working faster and less carelessly, it would be better to begin by redefining the sets as $A,M,B.$ However, below, I'm just sticking to the assigned set names, $A,B,C.$

• $30\%$ of all shoppers buy apples
• $45\%$ buy milk
• $40\%$ buy a loaf of bread
• probability that buys apples and milk is $0.20$
• probability that buys milk and bread is $0.25$
• probability that buys apples and bread is $0.12$
• probability that buys all three items is $0.07$

A Venn diagram (with the probabilities scaled by $100)$ can capture the above information. Start from the last bullet point and work upwards.

c) Find the probability that the shopper buys milk and bread but not apples.

c) $\mathbf{0.18}$

b) Find the probability that the shopper purchases none of the three items.

b) $\mathbf{0.35}$

a) Find the probability that the shopper purchases at least one of the three items.

a) $1-0.35=\mathbf{0.65}$ (alternatively, add up the numbers in the circles then divide by $100).$

Answer 2

Thanks to Henry for commenting that you actually have $~8~$ linear equations in $~8~$ unknowns, rather than only $~7~$ equations, as I originally wrote. I edited my answer accordingly.

---

Personally, when there are $~3~$ or more (basic) true/false conditions, giving rise to $~2^3 = 8~$ or more compound conditions, I prefer a truth table over a venn diagram.

I also regard the original poster's approach to be overly complicated and prone to errors.

\begin{array}{| r | r | r | r |} \hline \text{variable} & \text{apples} & \text{milk} & \text{bread} \\ \hline x_1 & \text{T} & \text{T} & \text{T} \\ \hline x_2 & \text{T} & \text{T} & \text{F} \\ \hline x_3 & \text{T} & \text{F} & \text{T} \\ \hline x_4 & \text{T} & \text{F} & \text{F} \\ \hline x_5 & \text{F} & \text{T} & \text{T} \\ \hline x_5 & \text{F} & \text{T} & \text{F} \\ \hline x_7 & \text{F} & \text{F} & \text{T} \\ \hline x_8 & \text{F} & \text{F} & \text{F} \\ \hline \end{array}

       x-1  x-2  x-3  x-4  x-5  x-6  x-7  x-8
E1 :    1    1    1    1    0    0    0    0   = 0.30
E2 :    1    1    0    0    1    1    0    0   = 0.45
E3 :    1    0    1    0    1    0    1    0   = 0.40
E4 :    1    1    0    0    0    0    0    0   = 0.20
E5 :    1    0    0    0    1    0    0    0   = 0.25
E6 :    1    0    1    0    0    0    0    0   = 0.12
E7 :    1    0    0    0    0    0    0    0   = 0.07
E8 :    1    1    1    1    1    1    1    1   = 1.0

The above tableau uses the problem's premises to create 8 linear equations in the 8 unknowns, $~x_1, \cdots, x_8,~$ based on the table. Note that equation E8 is implied by the fact that exactly one of the mutually exclusive events represented by $~x_1, \cdots, x_8~$ must occur.

At this point, you don't know for sure that the problem is solvable, because you don't know whether the $~8~$ equations are independent of each other. However, it is reasonable to presume, based on the perceived intent of the problem composer, that the problem is solvable.

Edit
If you are familiar with matrix theory, and you construct the $~8 \times 8~$ matrix represented by the above tableau, and you then find that the determinant of the matrix is non-zero, you would then have a guarantee that the problem is solvable. However, I regard that analysis as overkill, for this problem.

You are being asked (in effect) to compute

$$1 - x_8 = x_1 + \cdots + x_7.$$

So, let's start with what can be derived:

• Using E2 and E4,
  $x_5 + x_6 = 0.25.$

• Using E1 and E4,
  $x_3 + x_4 = 0.10~$ and
  $x_1 + x_2 = 0.20.$

So, the entire problem has been reduced to computing $~x_7.~$

However, from the table, I see no way of directly computing $~x_7.~$

So, I will try a different approach.

• Using E7 and E4,
  $x_1 = 0.7, ~x_2 = 0.13.$

• Then, since $~x_1~$ is known,
  using E6 and E5,
  $~x_3 = 0.05, ~x_5 = 0.18.$

Now, the problem can be directly conquered.

Since $~x_1, ~x_3, ~$ and $~x_5~$ are known, E3 may be used to compute

$$x_7 = 0.10.$$

Therefore, from the previous results, you have that

$$(x_1 + x_2) = 0.20, ~(x_3 + x_4) = 0.10, ~(x_5 + x_6) = 0.25, ~x_7 = 0.10.$$

Therefore,

$$x_1 + \cdots + x_7 = 0.65 \implies x_8 = 0.35.$$

Also, the probability of buying both milk and bread, but not apples, is represented by

$$x_5 = 0.18.$$

Answer 3

I think that you are assuming independence (isn't that why you're multiplying probabilities), and also you might be misunderstanding what the problem is telling you.

I think the set-up is as follows, depicted as a Venn diagram, despite user2661923's relative distaste for those. :-)

The various facts of the question tell you

• apples: $b+e+f+h = 30$
• milk: $c+e+g+h = 45$
• bread: $d+f+g+h = 40$
• apples and milk: $e+h = 20$
• apples and bread: $f+h = 12$
• milk and bread: $g+h = 25$
• apples, milk, and bread: $h = 7$
• law of probability: $a+b+c+d+e+f+g+h = 100$

You'll need to figure out what each of the eight variables are to answer the questions. It's easiest to work out from the center.