I've been experimenting with a graphing calculator and stumbled upon an interesting geometric construction involving functions and their normal lines. Here's the problem I'm trying to solve:
Let's consider a differentiable function $ f$ defined on a closed interval. For a given positive real number $ r > 0 $, we perform the following construction for every point $ (x, f(x)) $ on the graph of $ f $:
List item
- Draw the normal line to the graph of $ f $ at the point $ (x, f(x)) $.
- From the points on this normal line, select the one that is a distance $ r $ away from $ (x, f(x)) $ and has a $ y $-coordinate greater than $ f(x) $. If there are two such points with equal $ y $-coordinates, choose the one with the smaller $ x $-coordinate.
The result of this process is a new curve, which I'll denote as $ F $. This curve is not necessarily a function.
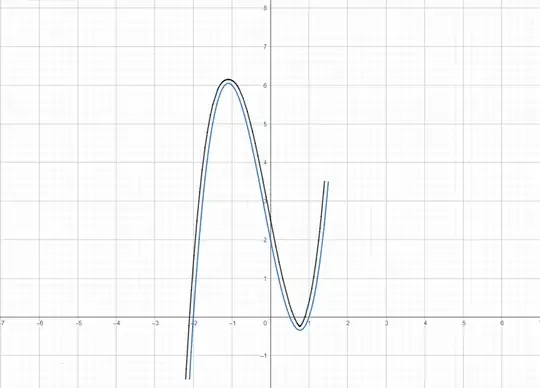
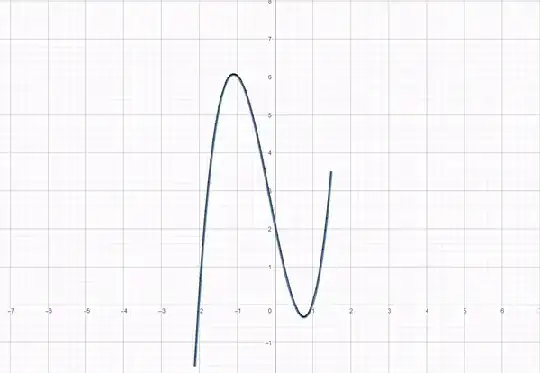
For instance, consider the function $ f(x) = (x-1)(x+2)(2x-1) $ with $ r = 0.1 $. The resulting curve from the above mapping is shown below:
Additionally, here's an animation showing the function $ f(x) = (x-1)(x+2)(2x-1) $ with $ r $ varying between $ 0 $ and $ 2 $, and the corresponding curve $ F $:
My question is: How can we mathematically determine the curve $ F $ given the function $ f $ and the distance $ r $?
This problem appears to be quite challenging, especially for ugly functions like the antiderivative of the Weierstrass function. Any insights or methods to approach this would be greatly appreciated.