What is the largest ellipse of given eccentricity that can be inscribed into square?

Question

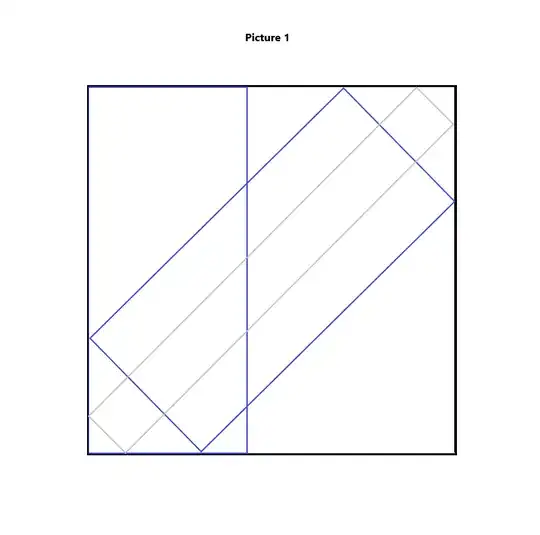
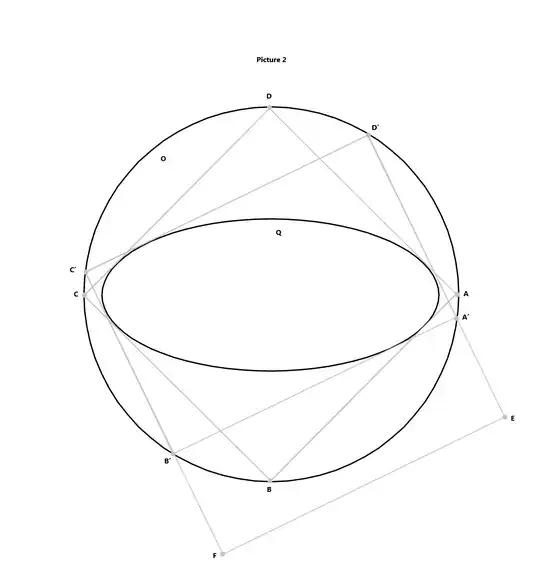
If eccentricity of ellipse is known, what is the position of the biggest such ellipse that can be inscribed into square? I could find the answer on the web – the biggest ellipse is positioned with its axes parallel to diagonals of the square, touching all four sides of the square. But no proof of this fact was given. I provide below my own proof of this statement.

Answer 1

• Considering the following Lissajous ellipse, $\theta \in (0,180^\circ)$:

$$\sin^2 \theta=x^2-2xy\cos \theta+y^2$$

• Ellipse area

$$A=\pi \sin \theta$$

• As $\theta$ varies, we have only one degree of freedom to inscribe an ellipse by a given square regardless the eccentricity of an ellipse. The largest ellipse should be a circle when $\theta=90^\circ$.

• Semi-axis lengths

$$\sqrt{2} \cos \frac{\theta}{2}$$

$$\sqrt{2} \sin \frac{\theta}{2}$$

• Eccentricity

$$e= \begin{cases} \sqrt{1-\tan^2 \frac{\theta}{2}}, & \quad \text{for} \quad \theta \in (0, 90^\circ) \\ \\ \sqrt{1-\cot^2 \frac{\theta}{2}}, & \quad \text{for} \quad \theta \in [90, 180^\circ) \end{cases}$$

• Combining both cases

$$4(1-e^2)=(2-e^2)^2(x^2+y^2) \pm 2x y (2-e^2)e^2$$

• Fixing eccentricity gives one kind of ellipse with two possible orientations.

• Please refer to my older post for Lissajous ellipse here.

Answer 2

It is interesting to note that position of the biggest ellipse of given eccentricity inscribed into square does not depend on eccentricity, although it is not the case for position of the biggest rectangle, with given ratio of its biggest to smallest sides, which can be inscribed into square. If rectangle is “thin” like grey one in $picture 1$ (ratio of lengths of biggest to smallest sides is high), it will be positioned along diagonal of the square, if rectangle is “fat” (ratio is close to $1$), it will be positioned with its shorter sides parallel and touching opposite sides of rectangle. If a square has side length $1$, the brake-even rectangle with sides $1$ and $ sqrt{2} – 1$ can be inscribed into square both with its sides parallel to diagonals of rectangle and with its sides parallel to sides of rectangle as shown in $picture 1$ below.

Proving that the biggest ellipse of any given eccentricity inscribed into square is positioned with its axes parallel to diagonals of the square is equivalent to proving that the smallest square, in which ellipse of given eccentricity is inscribed, is the one with its diagonals coinciding with axes of ellipse.

Consider arbitrary ellipse $Q$ and its director circle $O$, shown in $picture 2$. Director circle is a locus of all points from which ellipse is viewed at $90°$ angle. Let point $A$ be on a major axis of ellipse $Q$, if we draw lines $AB, BC, CD$ tangent to ellipse, encompassing it clockwise, with points $B,C,D$ on circle $O$, because $AC$ will be a diameter of circle $O$ (since $∠ABC$ is $90°$), it follows that $∠CDA$ is $90°$ and $AD$ is tangent to ellipse $Q$, so that we created a rectangle $ABCD$, in which ellipse $Q$ is inscribed, moreover, because $A$ is on major axis of ellipse and director circle shares center with its ellipse, it follows that points $B,D$ are on minor axis of ellipse and $ABCD$ is a square.

If for every possible position of point $A’$ on circle $O$ we create rectangle $A’B’C’D’$ through same steps as we did for square $ABCD$, we will create a set $S$ of all possible rectangles, in which ellipse $Q$ is inscribed, while touching all four sides of these rectangles. If for each rectangle $A’B’C’D’$ in set $S$ we create a square $EFC’D’$, extending the short side of $A’B’C’D’$ to the length of its long side, as shown in $picture 2$, we will create a set $T$ of all possible squares in which ellipse $Q$ is inscribed, while touching three sides of these squares. To prove our statement it is enough to prove that among all squares in set $T$ square $ABCD$ is the smallest, because any square in which ellipse is inscribed, while touching less than three sides, can either be reduced in size while containing same ellipse, or, if ellipse touches two opposite sides of that square, ellipse can be shifted within that square parallel to these sides, so that it start touching three sides of that square. We note that because all right triangles $A’C’D’$ have the same length of hypotenuse $A’C’$ - diameter of director circle $O$, and all corresponding squares in set $T$ have side length equal to the length of the longest cathetus among $C’D’, D’A’$, it follows that among all squares in set $T$, the smallest one is $ABCD$ and that proves our statement.