Find the radius of the red circle

Question

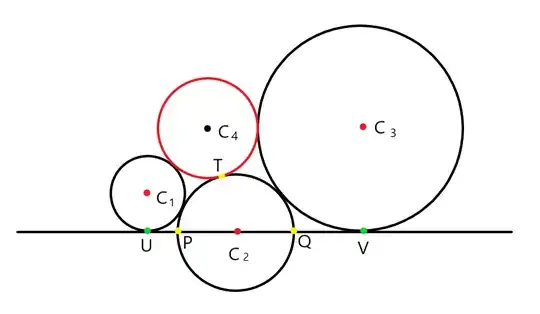
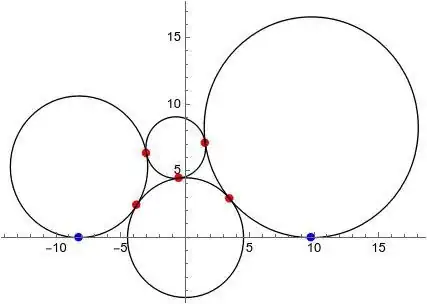
Four circles are arranged as shown in the figure below. They're numbered from $1$ to $4$. If the diameter of circle $C_2$ is equal to $9$, and $ PT = 6 , QT = 3 \sqrt{5} $. It is also given that $UV = 18$. Find the radius of the red circle.

My attempt:

Let the center $C_2 = (0,0)$, and let $UP = a$ and $QV = b$, and let $r_i$ be the radius of the $i$-th circle, then we have $r_1, r_3, r_4$ unknown , while $r_2 = 4.5 $. The coordinates of $C_i$ are

$ C_1 = (-4.5 - a, r_1) $

$C_2 = ( 0, 0) $

$ C_3 = (4.5 + b , r_3 )$

$ C_4 = (x_4, y_4) $

Now we write $5$ equations stemming from the distance formula relating the squared distances between pairs of centers chosen out the $4$ circles, and the square of the sum of their radii.

Taking the following pairs of circles: $(1, 2), (2, 3), (1, 4), (2, 4), (3, 4) $ gives us

$ (4.5 + a)^2 + r_1^2 = (r_1 + 4.5)^2 \tag{1} $

$ (4.5 + b)^2 + r_3^2 = (r_3 + 4.5)^2 \tag{2} $

$ (4.5 + a + x_4)^2 + (y_4 - r_1)^2 = (r_1 + r_4)^2 \tag{3}$

$ x_4^2 + y_4^2 = (4.5 + r_4)^2 \tag{4}$

$ (4.5 + b - x_4)^2 + (y_4 - r_3)^2 = (r_3 + r_4)^2 \tag{5}$

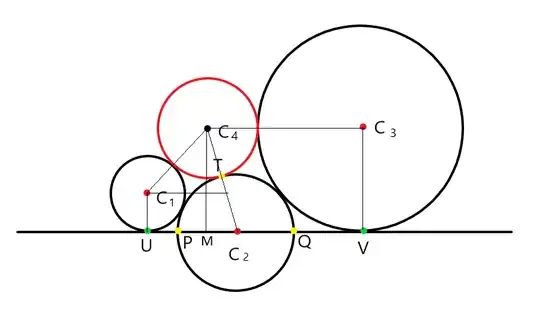
In addition to these five equations, we know that point $T$ is given by

$ T = P + PT ( \cos \phi, \sin \phi ) $

Where $ \cos \phi = \dfrac{PT}{PQ} = \dfrac{6}{9} = \dfrac{2}{3} $, therefore, $\sin \phi = \dfrac{\sqrt{5}}{3} $

Therefore,

$ T = (-4.5, 0) + 6 ( \dfrac{2}{3} , \dfrac{\sqrt{5}}{3} ) = (-0.5 , 2 \sqrt{5} ) $

It follows that

$ C_4 = \left(\dfrac{ r_4 + 4.5 }{4.5}\right) T $

And this reads

$ x_4 = - 0.5 (1 + \dfrac{2}{9} r_4 ) \tag{6}$

$ y_4 = 2 \sqrt{5} (1 + \dfrac{2}{9} r_4 ) \tag{7}$

With this equation $(4)$ becomes redundant.

And finally we have

$ a + b = 9 \tag{8}$

Now, equations $(1),(2), (3), (5)$ after expansion, become:

$9 a+ a^2 = 9 r_1 \tag{9} $

$ 9 b + b^2 = 9 r_3 \tag{10} $

$ 4.5^2 + a^2 + x_4^2 + 9 a + 9 x_4 + 2 a x_4 + y_4^2 - 2 y_4 r_1 = 2 r_1 r_4 + r_4^2 \tag{11} $

$ 4.5^2 + b^2 + x_4^2 + 9 b - 9 x_4 - 2 b x_4 + y_4^2 - 2 y_4 r_3 = 2 r_3 r_4 + r_4^2 \tag{12} $

Substituting equations $(9)$ and $(10)$ into $(11)$ and $(12)$ gives

$ 4.5^2 + 9 r_1 + x_4^2 + y_4^2 + 9 x_4 + 2 a x_4 - 2 y_4 r_1 = 2 r_1 r_4 + r_4^2 \tag{13}$

$ 4.5^2 + 9 r_3 + x_4^2 + y_4^2 - 9 x_4 - 2 b x_4 - 2 y_4 r_3 = 2 r_3 r_4 + r_4 ^ 2 \tag{14}$

So our system of equations is given by equations $(6), (7), (8)$ which are linear and equations $(9), (10), (13), (14)$ which are quadratic.

What remains is to how to solve these equations.

So the question here is: Are there further simplifications that can render this system of equations solvable?

I appreciate your input on this.

Edit: I found a reduction that can prove helpful. Subtracting equation $(10)$ from $(9)$, we get

$ 9 (a - b) + (a - b)(a+b) = 9 r_1 - 9 r_3 $

But $ a + b = 9 $, therefore,

$ 18 (a - b) = 9 (r_1 - r_3) $

i.e.

$ 2 (a - b) = r_1 - r_3 \tag{15} $

which is linear in the variables. So now we have $4$ linear equations which are equations $(6),(7),(8),(15)$ and three quadratic equations which are equations $(9), (13), (14)$.

Answer 1

Let's call the radii, respectively, $r_1, r_2, r_3, r_4$, where $r_2=4.5$ is already known to us. Moreover, assume $\angle C_4C_2P= \theta$ and $|UP|=x.$ By the length values given, it's very easy (please be aware that $C_4$, $C_2$, and $T$ are collinear) to get $\cos \theta=\frac{1}{9}$ and $\sin \theta =\frac{4\sqrt 5}{9}$.

Now, note that:

$$|C_1C_4|=r_1+r_4, \\ |C_2C_4|=4.5+r_4, \\ |C_4M|=(4.5+r_4)\sin \theta=(4.5+r_4)\frac{4\sqrt 5}{9}.$$

And,

$$=(|C_4M|-r_1)^2+(|UC_2|-|C_2C_4| \cos \theta)^2=|C_1C_4|^2.$$

Hence,

$$((4.5+r_4)\frac{4\sqrt 5}{9}-r_1)^2+(4+x-\frac{r_4}{9})=(r_1+r_4)^2. \ \ \ \ (1)$$

Similarly,

$$((4.5+r_4)\frac{4\sqrt 5}{9}-r_3)^2+(14-x+\frac{r_4}{9})=(r_3+r_4)^2. \ \ \ \ (2)$$

On the other hand, note that:

$$|C_1C_2|^2-|C_1U|^2=|C_2U|^2.$$

Hence,

$$(4.5+r_1)^2-r_1^2=(4.5+x)^2. \ \ \ \ (3)$$ Similarly,

$$(4.5+r_3)^2-r_3^2=(13.5-x)^2. \ \ \ \ (4)$$

By some help from Wolfram Alpha to solve $(1), (2), (3), $ and $(4)$, we have:

$$r_4 \approx 2.31, \\ r_3 \approx 8.29, \\r_1 \approx 5.32.$$

Remark 1: In the picture above we indeed have: $r_1=a, r_3=c,$ and $r_4=d$.

Remark 2: The numbers are very compatible with the figure posted by Jean Marie.

Answer 2

The method I present is motivated by having the less possible number of parameters (mainly parameter $r$ as defined below). It gives good approximate answers for the looked-for radius of circle $C_4$ ; here is for example what I obtain :

$$R\approx \frac92 0.51397634 = 2.31289354$$

in excellent coincidence with the exact value found by @mathlove.

Here are the different steps [this "stack" of different methods has the interest for the reader to be re-usable for more or less similar issues] :

• 0. First of all, for simplification, I make a uniform "down-scaling" with ratio $2/9$ of the figure by considering that circle $C_2$ becomes the unit circle.
• 1. It is not difficult to see with the given value for $PT$ that the coordinates of the point of tangency $T$ of circles $C_2$ and $C_4$ are :

$$T = \left(-\frac19, \ \frac{4\sqrt{5}}{9}\right)\tag{1}$$

• 2. I take geometrical inversion with respect to this circle $C_2$, which, expressed with complex numbers, is :

$$z=re^{i\theta} \ \mapsto \ \frac{1}{\overline{z}}=\frac{1}{r}e^{i\theta}\tag{2}$$

exchanging in particular externally tangent circles into internaly tangent circles with names $C'_1, C'_3,C'_4$ ($C_2$ remaining evidently inchanged). Let lowercase letters $c'_1, \ c'_3, \ c'_4$ be given to their centers, and their radii $r'_1, \ r'_3, \ r'_4$.

The resulting figure is given below.

Fig. 1: The figure has undergone a down-scaling $2/9$ in order that (inversion) circle $C_2$ the unit circle. The numbers at the bottom left are the values of $R$ and the error)

Let $r$ be the radius of $C'_4$. This will be the "guiding parameter" in the sequel.

Using (1), the coordinates of the center of $C'_4$ are

$$(a,b):=\left(-(1-r)\frac19, \ (1-r)\frac{4\sqrt{5}}{9}\right)\tag{3}$$

• 3. Then I use the fact that circles $C'_1$ and $C'_3$ belong to a parametrizable family of circles as described in a question of mine here (see formula (2) in the latter answer).

This parameterization allows to express the tangency of $C'_4$ and $C'_1$ by equating distance $c'_4c'_1$ and the sum of radii $r+r'_1$ ($r'_1$ being the radius of circle $C'_1$) :

$$\left(a-\tfrac{T^2-1}{(1+T)^2}\right)^2+\left(b-\tfrac{2T}{(1+T)^2}\right)^2=\left(\tfrac{2T}{(1+T)^2}+r\right)^2\tag{4}$$

Parameter $T$ associated with "twin circle" $C_3$ verifies evidently the same equation.

Reduction of (4) to a common denominator yields a polynomial equation which boils down (for a given value of parameter $r$) to a quadratic equation with 2 real roots : $T_1$ for $C'_1$ and $T_3$ for $C'_3$ (see SAGE program below) ; for example, if we take $r=1/4$, we get the following equation :

$$ \tfrac13(5T^2 - 4\sqrt{5}T - 6T + 4)(T + 1)^2=0$$

(where $(T + 1)^2$ is a spurious factor)

• 4. It remains to introduce the last constraint about distance $IJ = \frac29 18=4$ (where we recognize our scaling factor $\frac29$). Due to the definition of inversion (2), distance $IJ$ is plainly :

$$\frac{1}{|x_1|}+\frac{1}{|x_3|}=4 \tag{4}$$

where $x_1, x_3$ are the abscissas of centers $C'_1, C'_3$ resp.

The task now is to "adjust" the value of $r$ in such a way that (4) is fulfilled (see SAGE program below with $r$ value in the second line)

SAGE program for the figure :

    var('T')
    r=25344592/100000000
    fac=9/2
    def f(x,y,Rad,col,xt,yt,blah) : # circle plotting
        return point((x,y),color=col)+circle((x,y),Rad,color=col)+text(blah,(xt,yt),color=col)
    g=f(0,0,1,'green',0.75,-0.2,'C2') # unit circle
    Tx=-1/9;Ty=sqrt(80)/9
    xc=(1-r)*Tx;yc=(1-r)*Ty
    g+=f(xc,yc,r,'red',-0.2,0.7,"C'4")
    R=(1/(1-2*r)-1)/2
    g+=f((1+R)*Tx,(1+R)*Ty,R,'red',-0.2,1.8,"C4")
    p=(xc*(1+T)^2-(T^2-1))^2+(yc*(1+T)^2-2*T)^2-(2*T+r*(1+T)^2)^2
    s=p.roots(ring=AA,multiplicities=False) 
    dIJ=0
    for k in [1,2] : # index k=0 not considered : trivial root T=-1
       T=s[k]  
       xc1=(T^2-1)/(1+T)^2;yc1=2*T/(1+T)^2 # coord. center c1
       n1=sqrt(xc1^2+yc1^2)
       c1x=xc1/n1;c1y=yc1/n1
       R1=(1/(1-2*yc1)-1)/2
       if k==1 : # circles C1 and C'1
          g+=f(xc1,yc1,yc1,'blue',-0.75,0.3,"C'1")
          g+=f(c1x*(1+R1),c1y*(1+R1),R1,'blue',-1.2,0.3,"C1")
          g+=text("I",(c1x*(1+R1),-0.2))
       if k==2 :  # circles C3 and C'3
          g+=f(xc1,yc1,yc1,'blue',0.65,0.3,"C'3")
          g+=f(c1x*(1+R1),c1y*(1+R1),R1,'blue',1.4,0.3,"C3")
          g+=text("J",(c1x*(1+R1),-0.2))
       dIJ=dIJ+1/abs(xc1)
    show(g)
    Rexact=R*fac;show(Rexact.n(31))
    error=fac*(dIJ-4)
    show(error)

Answer 3

Another solution.

Calling the common tangent points as

$$ P_t=\{p_{12},p_{14},p_{23}, p_{34}, p_{24}\} $$

and the four circles as

$$ C_i(p,p_i,r_i) = 0, \ \ \ i = 1,\cdots, 4 $$

where $p= (x,y)$ is a generic point, $p_i,\ i = 1,\cdots, 4$ denote the circle's centers and $r_i$ the corresponding radius. From the given data, we can easily obtain $p_{24}$ as well as a condition over $p_4$. Now the compatibility conditions are:

$$ \cases{ C_1(p_{12},p_1,r_1) = 0\\ C_1(p_{14},p_1,r_1) = 0\\ C_2(p_{12},p_2,r_2) = 0\\ C_2(p_{23},p_2,r_2) = 0\\ C_3(p_{23},p_3,r_3) = 0\\ C_3(p_{34},p_3,r_3) = 0\\ C_4(p_{14},p_4,r_4) = 0\\ C_4(p_{24},p_4,r_4) = 0\\ C_4(p_{34},p_4,r_4) = 0 } $$

and also defining now $\vec g_i = \nabla C_1(p, p_i,r_i)$

$$ \cases{ \vec g_1\times \vec g_2 = 0\ \ \text{at}\ \ p_{12}\\ \vec g_1\times \vec g_4 = 0\ \ \text{at}\ \ p_{14}\\ \vec g_3\times \vec g_4 = 0\ \ \text{at}\ \ p_{34}\\ \vec g_2\times \vec g_3 = 0\ \ \text{at}\ \ p_{23} } $$

With this formulation we obtain a system of $13$ equations in $13$ unknowns to solve with the help of the attached MATHEMATICA script.

r2 = 9/2;
cc1 = (x + r2)^2 + y^2 - 6^2;
cc2 = (x - r2)^2 + y^2 - 45;
p = {x, y};
p4 = {x4, y4};
sol = Solve[{cc1 == 0, cc2 == 0}, {x, y}][[2]];
pT = p /. sol;
pU = {-u, 0};
pV = pU + {18, 0};
pO = {0, 0};
circ[p_, p0_, r_] := (p - p0) . (p - p0) - r^2
cross[u_, v_] := u[[2]] v[[1]] - u[[1]] v[[2]]
rel = cross[p4 - pO, pT - pO];
resx4 = Solve[rel == 0, x4][[1]];
p4 = p4 /. resx4;
p1 = pU + {0, r1};
p3 = pV + {0, r3};
c1 = circ[p, p1, r1];
c2 = circ[p, pO, r2];
c3 = circ[p, p3, r3];
c4 = circ[p, p4, r4];
gr1 = Grad[c1, p];
gr2 = Grad[c2, p];
gr3 = Grad[c3, p];
gr4 = Grad[c4, p];
p12 = {x12, y12};
p14 = {x14, y14};
p23 = {x23, y23};
p34 = {x34, y34};
rels1 = {
   circ[p12, p1, r1],
   circ[p14, p1, r1],
   circ[p12, pO, r2],
   circ[p23, pO, r2],
   circ[p23, p3, r3],
   circ[p34, p3, r3],
   circ[p14, p4, r4],
   circ[pT, p4, r4],
   circ[p34, p4, r4]
   };
rels2 = {
   cross[gr1, gr2] /. Thread[p -> p12],
   cross[gr1, gr4] /. Thread[p -> p14],
   cross[gr3, gr4] /. Thread[p -> p34],
   cross[gr2, gr3] /. Thread[p -> p23]
   };
equs = Join[rels1, rels2] // FullSimplify
vars = Variables[equs]
Length[vars]
Length[equs]
inits = {{r1, 5.}, {r3, 8.}, {r4, 2.}, {u, 8.}, {x12, -2.}, {x14, -2.}, {x23, 3.}, {x34, 2.}, {y12, 2.}, {y14, 6.}, {y23, 3.}, {y34, 7.}, {y4, 6.}};
sol = FindRoot[equs == 0, inits]
pts1 = {p12, p14, pT, p23, p34} /. sol;
pts2 = {pU, pV} /. sol;
gr0 = ListPlot[pts1, PlotStyle -> {PointSize[0.02], Red}];
gr0a = ListPlot[pts2, PlotStyle -> {PointSize[0.02], Blue}];
gr1 = Graphics[{Circle[{0, 0}, Abs[r2]], Circle[p1, Abs[r1]], Circle[p3, Abs[r3]], Circle[p4, Abs[r4]]} /. sol];
Show[gr0, gr0a, gr1, PlotRange -> All, AspectRatio -> 0.71]