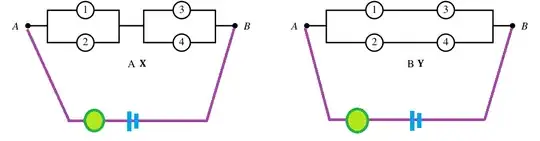
From Mathematical Statistics, 7th ed., Chapter 2, Supplementary Exercise no. 2.163:
Relays used in the construction of electric circuits function properly with probability $0.9$.
Assuming that the circuits operate independently, which of the following circuit designs yields the higher probability that current will flow when the relays are activated?
Assuming by "relays" they mean the circles with numbers inside of them (I am not very experienced with Electrical Engineering), I see how this is an exercise meant to test your understanding of conditional probabilities, but I'm having some trouble. For instance:
- Is it reasonable to assume that, say, circuit $A$ is functioning properly if and only if all of its relays are working?
- It seems like in circuit $B$, relays $3$ and $4$ are dependent on relays $1$ and $2$, but in circuit $A$ relays $3$ and $4$ are both dependent on $1$ and $2$. Is this likely what they're going for?
It also seems reasonable to say for both circuits that relays $1$ and $2$ are independent, as well as relays $3$ and $4$ are independent.
And from here, I'm not sure where to go. Any help is appreciated!