3

I am sure you all heard of this viral story: https://www.popularmechanics.com/science/math/a43469593/high-schoolers-prove-pythagorean-theorem-using-trigonometry/

It is certainty a new proof, however, what exactly does it mean "with trigonometry?". Using the Law of Cosine is circular, as its proof depends on the Pythagorean Theorem. However, it is not difficult to come up with a purely trigonometric proof that avoids identities that rely on the Pythagorean Theorem. It is quite easy to come up with such a proof.

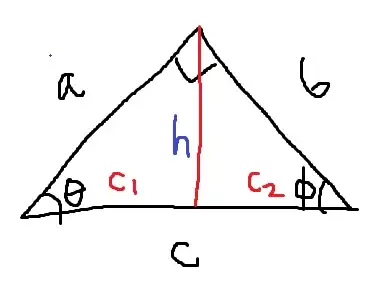
For example, consider the figure below,

enter image description here

We have that, $$\cos(\theta) = \frac{c_1}{a}, \cos(\phi) = \frac{c_2}{b}$$ We also have that, $$ \cos(\theta) = \frac{a}{c}, \cos(\phi) = \frac{b}{c} $$ By equating these we find that, $$ \frac{c_1}{a} = \frac{a}{c} \text{ and } \frac{c_2}{b} = \frac{b}{c} $$ This implies that $c c_1 = a^2$ and $c c_2 = b^2$. By adding these equations together we obtain that $c^2 = a^2 + b^2$.

So I just produced a proof for you using trigonometry only. Therefore, I find it as a silly claim that these high schoolers produced the first ever non-circular trigonometric proof in history. What they discovered is a new proof. In fact, you can argue their proof is much more interesting as it takes advanced of infinite series.

Thus, my question is what exactly do we mean by "first trigonometric proof"? It appears it is just a misleading headline by authors of the news who are unfamiliar with mathematics.

Nicolas Bourbaki
  • 5,553
  • 1
    That's a lot to read before you get to your question. – Thomas Andrews May 07 '24 at 00:15
  • 3
    @ThomasAndrews And if I asked my question directly some upset mod will close the question for "not enough context". So not matter what I ask will always result in people being upset. – Nicolas Bourbaki May 07 '24 at 00:18
  • 3
    This is not trigonometry. This is a proof by similar triangles, one which has been around since Euclid. – Ted Shifrin May 07 '24 at 00:18
  • It depends on who "we" stands for. As far as I am concerned, the whole story is just hot air. – Moishe Kohan May 07 '24 at 00:18
  • @TedShifrin Yes, and similar triangles is just a different way of re-writing a sine and cosine. – Nicolas Bourbaki May 07 '24 at 00:19
  • Oh, so using the definition of sin and cos is a trigonometric proof? Puleeeze. – Ted Shifrin May 07 '24 at 00:20
  • Not true, it is fine to put context after the question. @NicolasBourbaki – Thomas Andrews May 07 '24 at 00:22
  • 1
    @TedShifrin Then you are being logically inconsistent. The high schoolers use the "law of sines", which is nothing more than a manipulation of similar triangles and rewriting the definition of sine in those terms. So that is perfectly okay, and counts as "trigonometry"? – Nicolas Bourbaki May 07 '24 at 00:22
  • Your goal should be to help people help you. You are asking them to read a lot before they know if the can and want to help you. Some people will stop reading who might want to help you, some people will read all the way to your question and find they can't or don't want to help you, wasting their time. – Thomas Andrews May 07 '24 at 00:25
  • 1
    @ThomasAndrews Which is exactly what I did. I asked my question, "what do we mean by using trigonometry only?". I provided further context. And then I conclude my question again with the same question after the context has been given. – Nicolas Bourbaki May 07 '24 at 00:27
  • 3
    For example, I read it and was wonder if the question was going to be, "Is there a way to make the proof non-circular." But this question is really a word question - what does it mean to be a trigonometric proof. – Thomas Andrews May 07 '24 at 00:27
  • 3
    Reporting about this result tends to cite Elisha Loomis' The Pythagorean Proposition, which declares that any "trig proof" of Pythagoras is inherently circular because it invokes $\sin^2x+\cos^2x=1$. In this context, a "trig proof" is tautologically one that (perhaps implicitly) uses the relation. People have since misconstrued Loomis' statement as a ban on any argument mentioning sine or cosine at all, which is silly. Using trig functions merely to name and manipulate ratios in a right triangle (as Johnson & Jackson did) is allowed. – Blue May 07 '24 at 02:01
  • 1
    @Blue Finally, somebody actually gave a meaningful reply. That makes sense. Basically, a trigonometric proof that avoids the Pythagorean Identity. If so, there are many other proofs one can give, most of them much simpler. – Nicolas Bourbaki May 07 '24 at 02:25
  • @NicolasBourbaki: The title of Popular Mechanics article you cite ---and thumbnails of videos from MathTrain and polymathematic and others--- suggests that trig proofs are "impossible". Yet, the article closes by noting "other mathematicians have employed similar approaches before". Certainly, J&J's approach is laudable for being clever, novel, and devised by high-schoolers; but all the hype and click-bait claims of "proving the impossible" does the teens a disservice. We should expect better from math/sci communicators. – Blue May 07 '24 at 03:28
  • 1
    @Blue I agree that all these articles, and videos, should simply be titled as "high-schoolers come up with a new proof of Pythagorean theorem". – Nicolas Bourbaki May 07 '24 at 03:41

0 Answers0