Dividing a polyhedron into two similar copies of itself

Question

The paper Dividing a polygon into two similar polygons provides that there are only three families of polygons that are irrep-2-tiles (can be subdivided into similar copies of the original).

Right angled triangles
$1:\sqrt{2}$ parallelograms
The Golden Bee

I wish to find examples of polyhedra that are irrep-2-tiles. The only example I have been able to find is:

The $1:2^\frac{1}{3}:2^\frac{2}{3}$ parallelopipeds.

Are there further examples? I would like to find as many as possible.

I have now posted this question on MathOverflow also.

Edit: A diagram of the Golden Bee from the linked paper. It seems plausible that there could be a $3d$ analogue.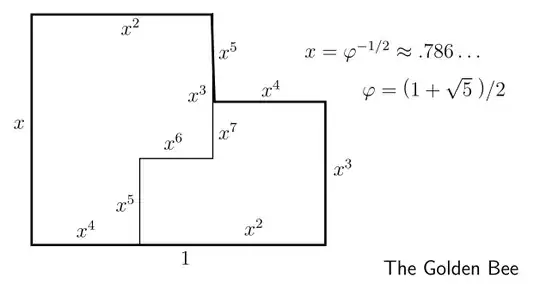

Addressing Jaap Scherphuis' comment, such a polyhedron would be able to tile $\mathbb{R}^3$, provided you used copies of different sizes. An analogue of the Pinwheel tiling would work.

However, I can't think of a way to guarantee that we only use a finite amount of different sizes of the tile. The "natural" tiling, adjoining copies of the polyhedron again and again to cover the entire plane will need arbitrarily large polyhedra. We can subdivide these to reduce their size, but unless we have some lucky scaling factors we'll end up with infinitely many different sizes of tile.

It would have to be a space-filling polyhedron since you could subdivide (and then scale up) indefinitely to tile an arbitrarily large region of space. I don't think there will be any others, since the other known space-filling polyhedra probably don't split like that. — Jaap Scherphuis, Apr 23 '24 at 10:02
@JaapScherphuis The polyhedrons would not necessarily be of the same size, so they would not have to be space-filling in the sense of the page you linked. — Kepler's Triangle, Apr 23 '24 at 10:25
The golden bee in the two dimensional case is a weird outlier, and makes me suspect there may be oddities in 3 dimensions as well. — Kepler's Triangle, Apr 23 '24 at 10:26
Did you try posting on mathoverflow? This seems to be very specialized knowledge. — Starlight, Apr 27 '24 at 03:20
I'll wait until the bounty runs out, then I'll try mathoverflow. — Kepler's Triangle, Apr 27 '24 at 09:22
See the related Question about polyhedra which can be split into self-similar pieces and its accompanying links, e.g. this older unanswered Question. — hardmath, Apr 27 '24 at 12:06
@hardmath Those questions are certainly related, but while there are lots of examples of rep-tiles of order 4 and greater as well as irreptiles of larger orders, the only example of an order 2 reptile they provide is the Delian brick, a special case of the parallelopipeds I mention above. — Kepler's Triangle, Apr 27 '24 at 12:53
From the your first link, it is certainly interesting that by the time you reach order 8 there are thousands of examples. — Kepler's Triangle, Apr 27 '24 at 12:54
Yes, the case of two self-similar parts is doubtless very restrictive in the 3D setting. — hardmath, Apr 27 '24 at 13:21
@Numeral I suspect that there's a specific explosion at order $8$ corresponding to the fact that similar copies of a polyhedron at $\frac18$th the volume will have $\frac12$ the edge length of the original, so there are many more plausible ways to do that than there would be for splitting into 2 or 4 equal pieces. — Steven Stadnicki, Apr 27 '24 at 22:31
@StevenStadnicki That's a good point. It seems more natural to find examples of shapes that can be subdivided into pieces half their original size, but I wonder if that can be made rigorous. Certainly cubes are of order 8, and a lot of known rep-tiles are composites of cubes. — Kepler's Triangle, Apr 27 '24 at 23:07

Dividing a polyhedron into two similar copies of itself

0 Answers0

Linked