The covering-space argument is described in the following picture:
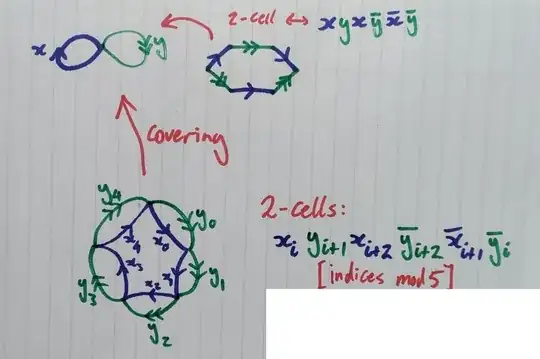
At the top we have a 2-complex, with fundamental group $B_3$. It is precisely the presentation complex of the presentation $\langle x, y\mid xyx=yxy\rangle$, so has $1$-skeleton as drawn on the left, and then we glue a $2$-cell on in the hopefully obvious way.
The subgroup defined in the question corresponds to the kernel of the map $B_3\to\mathbb{Z}_5$ defined by $\phi:x\mapsto 1, y\mapsto 1$, and hence clearly to an index-5 subgroup. This corresponds to a $5$-sheeted covering of our presentation complex. To draw this covering space, I first drew the Cayley graph of $\mathbb{Z}_5$, and for each of the $5$ vertices $0, \ldots, 4$ I added edges $x_i, y_i$ corresponding to the image of $\phi(x), \phi(y)$ at this point - in this case, $x_i$ and $y_i$ move to the next vertex, but for example the map $\psi:x\mapsto 1, y\mapsto0$ would have $x$-edges as here, but loop edges for each $y_i$. This gives us our $1$-skeleton. Then $2$-cells are then the lift of the $2$-cell of the presentation complex at of the $5$ vertices - that is, for each vertex $0, \ldots, 4$, read $xyxy^{-1}x^{-1}y^{-1}$ to get a $2$-cell. This gives:
$$\begin{align*}
x_0y_1x_2y_2^{-1}&x_1^{-1}y_0^{-1}\\
x_1y_2x_3y_3^{-1}&x_2^{-1}y_1^{-1}\\
&\vdots
\end{align*}
$$
To get the fundamental group of this covering space, which is what we are after, we take the presentation with the $1$-cells as generators, and then the $2$-cells and a then $1$-cells forming a spanning tree as relations; I suggest $y_1=1,y_2=1,y_3=1,y_4=1$ as the spanning tree. This gives a presentation as follows:
$$
\begin{align*}
\langle x_i, y_i, i\in\{0, \ldots, 4\}\mid x_iy_{i+1}x_{i+2}y_{i+2}^{-1}&x_{i+1}^{-1}y_i^{-1}\:(i \mod 5), y_1, \ldots, y_4
\rangle
\end{align*}
$$
Now write this out in full, remove the generators $y_1, \ldots, y_4$ from the presentation, and then carefully use Tietse transformations to reduce down to two generators. The result is the Braid group. [I can do this in full if needed, I'm just out of time now :-)]
