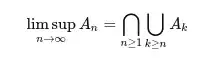2

Sorry if this is a stupid question, but I have been staring at this for too long and can't figure it out. This is from page 3 of "Stochastic Processes" by Sheldon Ross in the proof of the Borel-Cantelli Lemma. In the proof the "limit supremum" of a sequence of events (not necessarily increasing or decreasing) is defined as:

enter image description here

My question is: how is this event not equal to the empty set? The way I am looking at it: For each n, if k < n, then A_k is not in that union. Therefore if A_k is not in at least one of these unions, it's not in the intersection. Now, for every possible natural number k you can think of, there exists another number n > k. Therefore there exists a union which does not contain k, for each number k. Therefore none of the A_k are in this set. But according to the book this event is supposed to represent an infinite number of A_k occurring.

Where did my logic go wrong? Any help would be much appreciated!

Asaf Karagila
  • 405,794
Azi muth
  • 65
  • 2
    Well, most basically, if $x\in\bigcap_{n=1}^\infty A_n$ , then the $\limsup$ contains $x.$ More general, $x\in\limsup A_n$ if $x\in A_n$ for infinitely many $n.$ – Thomas Andrews Apr 02 '24 at 16:05
  • 5
    Your error appears to be in thinking of each $A_k$ as being either single element sets or having no overlap with other sets. Consider for instance the sequence of events (in interval notation) $(-1-\frac{1}{k},1+\frac{1}{k})$. The element $0.5$ is in all $A_k$ for instance. – JMoravitz Apr 02 '24 at 16:05
  • 1
    What if all the $A_k$ are the same set/event? In that case $\bigcup_{k \geq n} A_k = A_k$ for all $k$, so $\limsup_{n \to \infty} A_n = A_k$. Try and work through this example with your logic. – Ben Steffan Apr 02 '24 at 16:06
  • 1
    If $A_i\subseteq A_{i+1}$ for all $i,$ then $\limsup A_i=\bigcup_{i=1}^\infty A_i.$ – Thomas Andrews Apr 02 '24 at 16:09
  • 1
    Maybe of interest: https://math.stackexchange.com/questions/107931/lim-sup-and-lim-inf-of-sequence-of-sets – Hans Lundmark Apr 02 '24 at 17:01
  • THANK YOU so much everyone!! It's hard sometimes self-studying because I don't have a teacher per se to ask stuff, and I try to avoid asking until I've really thought about it for a while, but you guys always come through! <3 – Azi muth Apr 02 '24 at 17:32

0 Answers0