Why does conjugating one of the complex vectors in the inner product, still give the correct dot product?

Question

In the complex space, I understand that we need to conjugate one of the vectors in the dot product to avoid getting that <v,v> ≤ 0. What I am unable to understand, is how taking the dot product between w as shown in picture 1 and v conjugated still gives the correct dot product? How can the dot product of w and v conjugated still represent how closely the two vectors align, when we instead use the conjugated v? Is there some sort of interpretation of the complex plane that I'm missing? I´ve tried using the formula of multiplication between two complex numbers as in picture 2 (I don't know how to write formulas on the forum) and Euler's formula to maybe get a better understanding of how taking the inner product with the conjugated still ends up giving the correct relation and length if you take the norm. I think this makes sense if you take the inner product <v,v conjugated> as you'll end up getting |v|^2 and therefrom that the norm is equal to |v|. But this obviously won't work for the inner product <w,v conjugated> in general, as what I got was the result of the special case <v, w> where v=w. Hope this makes sense, thanks in advance!

Answer 1

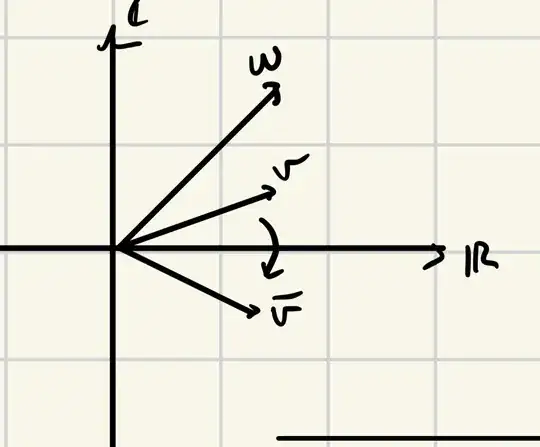
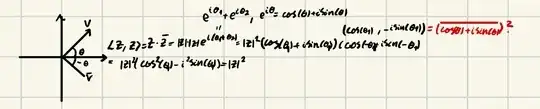We define the standard inner product on the vector space $\mathbb{C}$ over the field $\mathbb{C}$ as the function $\langle \cdot, \cdot \rangle: \mathbb{C} \times \mathbb{C} \to \mathbb{C}$ via $\langle \cdot, \cdot \rangle:(\boldsymbol{u}, \boldsymbol{v}) \mapsto \boldsymbol{u} \boldsymbol{\bar{v}}$. This notation can be cumbersome so we denote $\langle \cdot, \cdot \rangle((\boldsymbol{u},\boldsymbol{v}))$ as $\langle \boldsymbol{u},\boldsymbol{v} \rangle$. We can check that this satisfies the defining properties of an inner product (namely conjugate symmetry, linearity in the first argument, and positive-definiteness). The inner product $\langle \boldsymbol{w}, \boldsymbol{v}\rangle$ is computed as $\boldsymbol{w} \boldsymbol{\bar{v}}$ and not $\boldsymbol{w} \boldsymbol{v}$. It follows that the inner product between $\boldsymbol{w}$ and $\boldsymbol{\bar{v}}$ is $\langle \boldsymbol{w}, \boldsymbol{\bar{v}}\rangle = \boldsymbol{w} \boldsymbol{\bar{\bar{v}}}=\boldsymbol{w} \boldsymbol{v}$, which is not generally equal to the inner product between $\boldsymbol{w}$ and $\boldsymbol{v}$, $\langle \boldsymbol{w}, \boldsymbol{v}\rangle = \boldsymbol{w} \boldsymbol{\bar{v}}$.

I think a potential source of confusion is coming from introducing the "dot product" function $\cdot: \mathbb{C} \times \mathbb{C} \to \mathbb{C}$ via $\cdot:(\boldsymbol{u},\boldsymbol{v}) \mapsto \boldsymbol{u} \boldsymbol{v}$. It is important to note that $\cdot$ is not another inner product on the vector space $\mathbb{C}$ over $\mathbb{C}$ because it does not have the conjugate symmetry and positive-definiteness properties. However, one can write $\langle \boldsymbol{w}, \boldsymbol{v}\rangle=\boldsymbol{w} \cdot \boldsymbol{\bar{v}}$, meaning that the inner product of $\boldsymbol{w}$ and $\boldsymbol{v}$ is the dot product of $\boldsymbol{w}$ and $\boldsymbol{\bar{v}}$. It is incorrect though to say that the inner (dot) product of $\boldsymbol{w}$ and $\boldsymbol{v}$ is the inner (dot) product of $\boldsymbol{w}$ and $\boldsymbol{\bar{v}}$.

Therefore, the inner product of $\boldsymbol{v}$ and $\boldsymbol{\bar{v}}$ is not $\lvert \boldsymbol{v}\rvert^2$. It is $\boldsymbol{v}\boldsymbol{v}=\boldsymbol{v}^2$. The dot product of $\boldsymbol{v}$ and $\boldsymbol{\bar{v}}$ is $\lvert \boldsymbol{v}\rvert^2$. Distinguishing between the standard inner product and dot product is important here.