perpendicular lines through $F$ project to perpendicular lines

Question

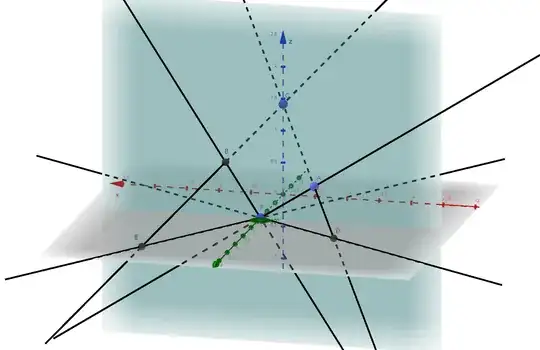
Let $C(0,0,\sqrt{2})$ and $F(0,\sqrt{2},0)$ be two points in $\Bbb R^3$.
$AF,BF$ are arbitrary perpendicular lines through $F$ on the plane $y=\sqrt{2}$.
These lines project to the lines $DF,EF$ under the perspective projection centered at $C$ onto $xy$-plane.
Then the lines $DF,EF$ perpendicular?

This question is based on the last sentence of this post about why perpendicular lines project to perpendicular lines.

I simplified the setting by an isometry $(x,\frac{y}{\sqrt{2}},\frac{-y}{\sqrt{2}},z)\mapsto(x,y,z)$ from the subspace $y+z=0$ of the $(x,y,z,w)$-space to the the $(x,y,z)$-space.

Then I generalized the question to make the angle $\alpha$ between two planes be arbitrary:

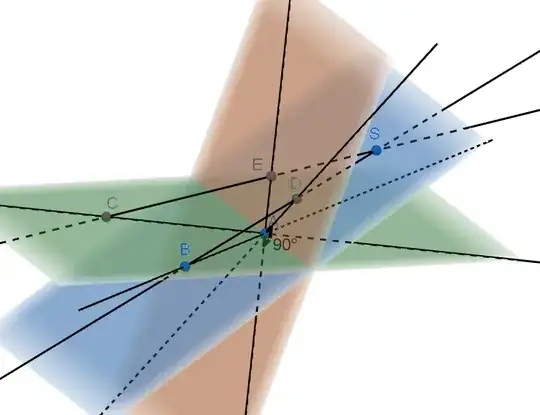
Let $\alpha\in(0,\frac\pi4)$ be arbitrary.
Let $A=(0,0,0),S=(0, 1,\tan(α))$ be two points in $\Bbb R^3$.
$BA,CA$ are arbitrary perpendicular lines through $A$ on the plane $z=0$.
These lines project to the lines $DA,EA$ under the perspective projection centered at $S$ onto the plane $z =\tan(2α) y$.
Then the lines $DA,EA$ are perpendicular?

Answer 1

Hint (for a strightforward but maybe a bit tedious solution):

You can choose points $A$ and $B$ to be given by $\vec a=\left(\cos\phi,\sqrt 2,\sin\phi\right)$ and $\vec b =\left(-\sin\phi,\sqrt 2,\cos\phi \right)$. The projection onto the $xy$ plane is then given by $\vec\alpha =P\vec a= \vec c +\mu \left(\vec a -\vec c\right)$, with $\mu$ chosen such that $\alpha_z=0$ , and similar for $\vec b$. Then you just need to show that $$\left(\vec f -\vec\alpha\right)\cdot\left(\vec f -\vec\beta\right)=0\,.$$

Answer 2

For the generalized question, we only need to prove that: When the plane $z=\tan(2\alpha)y$ rotates about the x axis to the plane $z=0$, the lines $BA,CA$ are images of $DA,EA$. Since rotation preserves angles, they remain perpendicular.

So the question becomes

$A$ is the point $(0,0,0)\in\Bbb R^3$.
$C$ is the point $(1,0,0)$.
$S$ is the point $(0,1,\tan(\alpha))$.
A line through $S$ intersects the planes $z=0$ and $z=\tan(2\alpha)y$ at $B,D$.
Then $AB$ and $AD$ form equal angles with $AC$

The question can be rephrased as:

Two planes $\Pi_1,\Pi_2$ intersect in the line $AC$.
$S$ is a point on the bisector plane $\Pi$ of the dihedral angle formed by $\Pi_1,\Pi_2$.
A line through $S$ intersects the two planes at two points $B,D$.
$A$ is the orthogonal projection of $S$ onto the line $AC$.
Then $AB$ and $AD$ form equal angles with $AC$.

Consider the plane $\rho$ through the lines $SA$ and $SBD$, it is an arbitrary plane through the line $SA$, since the line $SBD$ is an arbitrary line through $S$.

So the question can be rephrased as

Two planes $\Pi_1,\Pi_2$ intersect in the line $AC$.
$S$ is a point on the bisector plane $\Pi$ of the dihedral angle formed by $\Pi_1,\Pi_2$.
$A$ is the orthogonal projection of $S$ onto the line $AC$.
A plane $\rho$ through $SA$ intersects the two planes at two lines then they form equal angles with $AC$.

The dihedral angle formed by the planes $\Pi_1,\Pi_2$ has two bisector planes, one of them is $\Pi$, let the other one be $\Pi'$.

Consider the the reflection in $\Pi'$.
The planes $\Pi_1,\Pi_2$ are symmetric.
The plane $\Pi$ is mapped to itself, since it is orthogonal to $\Pi'$.
Since the line $SA$ lies in $\Pi$ and orthogonal to $AC$, it is orthogonal to $\Pi'$.
Since the plane $\rho$ contains the line $SA$, it is orthogonal to $\Pi'$, therefore mapped to itself.
The line $AB$ and $AD$ are symmetric since they are intersections of the plane $\rho$ with the planes $\Pi_1$ and $\Pi_2$.
Therefore the angle $\angle CAB$ is mapped to $\angle CAD$. Therefore $\angle CAB=\angle CAD$. QED