Construct perspective projection of rotating tesseract by perpendicular lines intersecting ellipse

Question

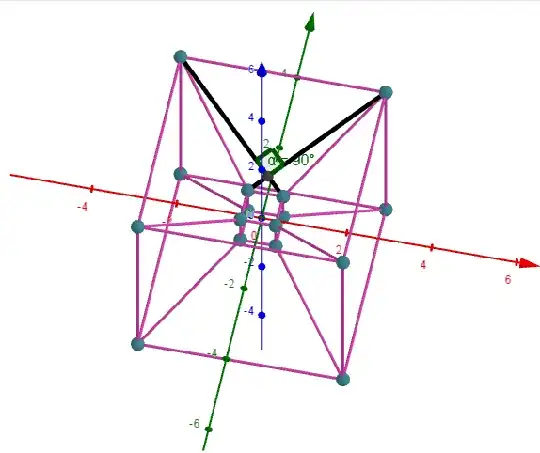
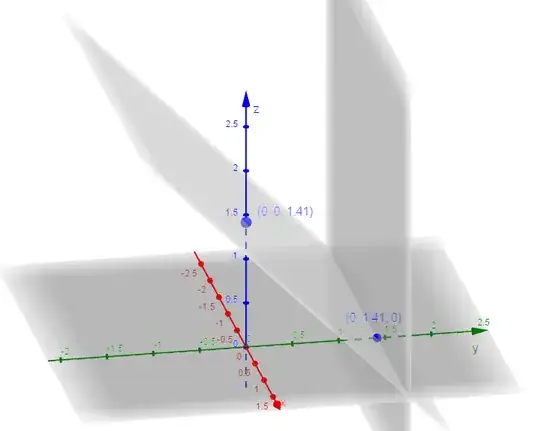
The contruction was used in two different sources on the web: a Geogebra resource and a video using inRm3D so I think it must be documented and proved somewhere, but I didn't find any.

Here is the construction (following the second source):

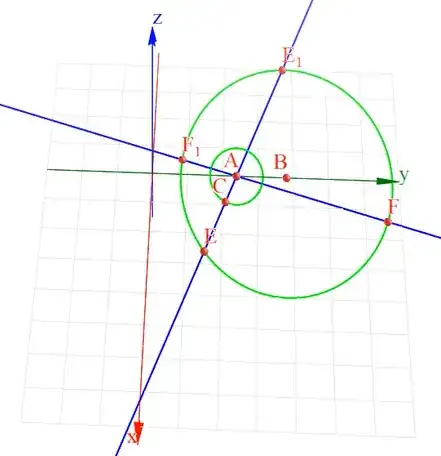
1. On the xy-plane, draw a conic symmetric about $y$-axis. (Ignore the small green circle, its only purpose is to rotate $C$ on it.)
2. Take a point $A$ on the $y$-axis.
3. Draw two perpendicular lines through $A$, intersecting the conic at $E,F,E_1,F_1$.
   
4. Rotate $E,F,E_1,F_1$ by $45+n⋅90$°,$(n=0,1,2,3)$ around the $x$-axis to get $16$ points in total:
   
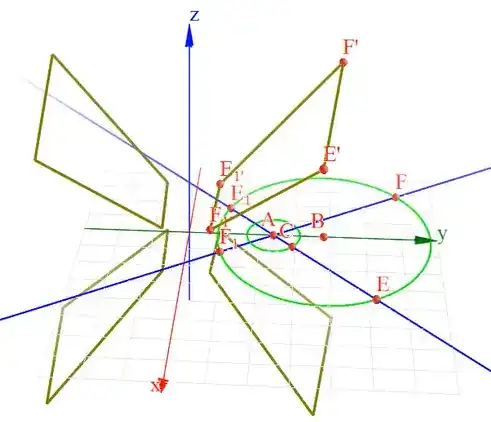
5. When the perpendicular lines rotate around $A$, the points $E, F, E_1, F_1$ will move on the ellipse, and he claimed that the 16 points will be a perspective projection of 16 vertices of the tesseract $\{(\pm1,\pm1,\pm1,\pm1)\}$ rotated about $xw$-plane.

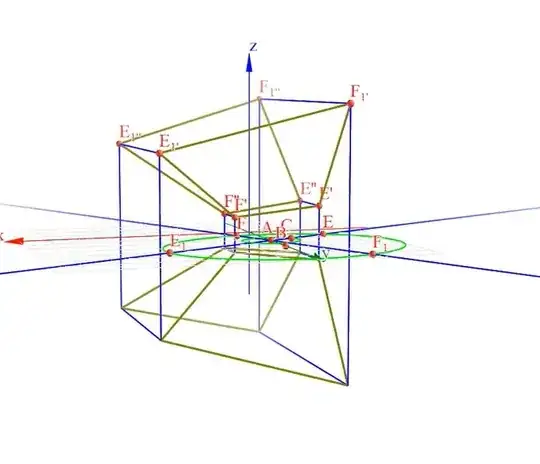
To verify this, I take $(0,0,0,\text{distance})$ as the center of projection (where $\text{distance}$ is a constant to be determined) and take the distance between the center of projection and the "view space" to be $1$ (changing this will just rescale the projection). So the "view space" is the 3-dimensional affine subspace $w=\text{distance}-1$. For example, the point $(0,1,-1,0)$ is projected to $(0,\frac1{\text{distance}},-\frac1{\text{distance}},\text{distance}-1)$ because the line through $(0,0,0,\text{distance})$ and $(0,1,-1,0)$ intersects $w=\text{distance}-1$ at $(0,\frac1{\text{distance}},-\frac1{\text{distance}},\text{distance}-1)$.

Then I compute the perspective projection of a 2D-face $P_2P_3P_{10}P_{11}$ of the tesseract rotated about $xw$-plane.
Mathematica code:

P2 = {{1}, {1}, {-1}, {1}}
P11 = {{-1}, {1}, {-1}, {-1}}
P10 = {{1}, {1}, {-1}, {-1}}
P3 = {{-1}, {1}, {-1}, {1}}
rotXW = {{Cos[angleXW], 0, 0, Sin[angleXW]}, {0, 1, 0, 0}, {0, 0, 1, 
   0}, {-Sin[angleXW], 0, 0, Cos[angleXW]}}
Q2 = rotXW . P2
Q11 = rotXW . P11
Q10 = rotXW . P10
Q3 = rotXW . P3
W2 = 1/(distance - Q2[[4, 1]])
M2 = {{W2, 0, 0, 0}, {0, W2, 0, 0}, {0, 0, W2, 0}}
W11=1/(distance-Q11[[4,1]])
M11={{W11,0,0,0},{0,W11,0,0},{0,0,W11,0}}
W10 = 1/(distance - Q10[[4, 1]])
M10 = {{W10, 0, 0, 0}, {0, W10, 0, 0}, {0, 0, W10, 0}}
W3=1/(distance-Q3[[4,1]])
M3={{W3,0,0,0},{0,W3,0,0},{0,0,W3,0}}
MP2=M2.Q2
MP11=M11.Q11
MP10=M10.Q10
MP3=M3.Q3
A2 = Transpose[MP2][[1]]
A11=Transpose[MP11][[1]]
A10=Transpose[MP10][[1]]
A3=Transpose[MP3][[1]]

The projection of the square $P_2P_3P_{10}P_{11}$ is $A_2A_3A_{10}A_{11}$, lying on the plane $y+z=0$.
The circumcircle of the square will project to the conic in Step $1$ of the construction.
To impose the relation $EE_1\perp FF_1$ in Step $3$ of the construction, let the diagonals of the square $A_2A_3A_{10}A_{11}$ be perpendicular: $A_2A_{11}\perp A_{10}A_3$, so I let the inner product be zero:

Dot[A2-A11,A10-A3]//FullSimplify

I get$$\frac{8 \left(\text{distance}^2-2\right) \cos (2\ \text{angleXW})}{\cos (4\ \text{angleXW})+2\ \text{distance}^4-4\ \text{distance}^2+1}$$ this always equal zero when $\text{angleXW}$ changes, so $\text{distance}^2-2=0$. I take $\text{distance}=\sqrt{2}$.
In GeoGebra I plot the exact coordinates:

and the diagonals are perpendicular as desired. But the issue in Step $1$ of the construction is that it uses an ellipse as the projection of the circumcircle of the square but my computation shows it should be a parabola:
Take an orthonormal basis $\{(1,0,0),\frac1{\sqrt2}(0,1,-1)\}$ of the plane $y+z=0$. Coordinates of $A_2$ is calculated above. Write it in our basis as $$A_2=a(1,0,0)+b\frac1{\sqrt2}(0,1,-1)$$ I find \begin{align}a&=\frac{\sin (\text{angleXW})+\cos (\text{angleXW})}{\sin (\text{angleXW})-\cos (\text{angleXW} )+\text{distance}}\\b&=\frac{\sqrt{2}}{\sin (\text{angleXW})-\cos (\text{angleXW})+\text{distance}}\end{align} Eliminating $\text{angleXW}$ I get$$2 a^2+b^2 \left(\text{distance}^2-2\right)-2 \sqrt{2} \text{distance}\ b+2=0$$So when $\text{distance}=\sqrt2$, the trajectory of $A_2$ as $\text{angleXW}$ varies is a parabola (also the trajectory of $A_{11},A_{10},A_3$) $$a^2-2 b+1=0$$ so the intersection of $A_2A_{11},A_{10}A_3$ is exactly the focus $(0,1)$ of the parabola.
Plotting in exact coordinates:

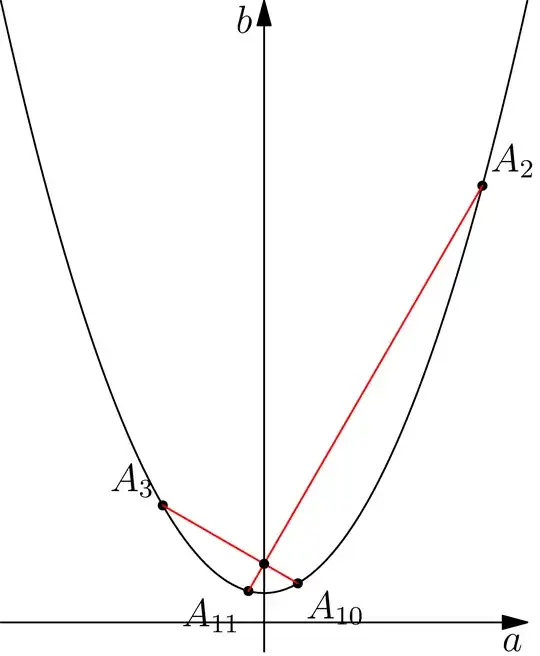
In Step $1$ of the construction, it uses an ellipse as the projection of the circumcircle of the square but my computation shows it should be a parabola. I am not sure about this. Also, is there a better way to show that the right angle at the center of the square is preserved by the perspective projection and $xw$-rotation when $\text{distance}=\sqrt{2}$?

Answer 1

Also, is there a better way to show that the right angle at the center of the square is preserved by the perspective projection and $xw$-rotation when $\text{distance}=\sqrt{2}$?

The center of the square $P_2P_3P_{10}P_{11}$ is $(0,1,-1,0)$.

In the post the "view space" is $w=\text{distance}-1$. We change this to $w=0$ (will just rescale the projection) then the point $(0,1,-1,0)$ lies on the "view space", so it will be fixed under this perspective projection.

To apply this post with the two planes (the original plane $P_2P_3P_{10}P_{11}$ and the image plane $A_2A_3A_{10}A_{11}$), we check the conditions are satisfied:

• First, $(0,1,-1,0)$ is the orthogonal projection of $(0,0,0,\text{distance})$ onto the intersection line of two planes;
• Second, the perspective center $(0,0,0,\text{distance})$ lies on a bisector plane of the two planes if and only if $\text{distance}=\pm\sqrt{2}$.

so the angle at $(0,1,-1,0)$ will be preserved, by that post.

---

In the figure below, the point $(x,\frac{y}{\sqrt{2}},\frac{-y}{\sqrt{2}},z)$ corresponds to the point $(x,y,z)$, which is an isometry.
So $(0,1,-1,0)$ corresponds to the point $(0,\sqrt{2},0)$,
the original plane corresonds to $y=\sqrt{2}$,
the image plane corresponds to $z=0$,
and the perspective center $(0,0,0,\sqrt{2})$ corresponds to $(0,0,\sqrt{2})$ which lies on a bisector plane of the two planes.