I have written a Python script that defines a meshgrid. The meshgrid represents a 3D grid in Cartesian (x, y, z) coordinates, and for each point, I want to apply a function. After applying the function to all points, I should obtain a vector field.
Firstly, I convert each given point to cylindrical coordinates using the following equations:
$$r = \sqrt{x^2+y^2}$$
$$\phi = \arctan\left(\frac{y}{x}\right)$$
Since my func takes cylindrical coordinates and returns cylindrical coordinates:
r, \phi, z = func(r, \phi, z)
I need to convert the coordinates back to Cartesian (x, y, z):
$$x = r\cos(\phi)$$ $$y = r\sin(\phi)$$
When I plot the points after running the script, the results are not as expected.
I defined func to be the magnetic field:
$$func(r, \phi,z) = \hat{\phi}\left(\begin{cases} \frac{R^2}{3\cdot r}& R\leq r\\ \frac{r^2}{3\cdot R} &r < R\end{cases}\right)$$
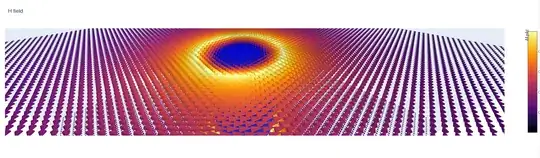
and is seems the convertion of vector back to Cartesian, ignores the magnitude of the rotation effect the magnetic field does. the result plot looks like that:

I achieve the expected result only after taking the return value of func as the new radius $(r)$ and defind the vectors with the following convertion: $(-r\cdot sin(t), r\cdot cos(t), 0)$:
funcfunction as $f_{\phi}$, then I need to solve this system of equations: $$\begin{cases} V_{x}\cdot\cos(t)+V_{y}\cdot\sin(t)=0\ -V_{x}\cdot\sin(t)+V_{y}\cdot\cos(t)=f_{\phi}\ V_{z}=0\end{cases}$$ I then plot the vector $\vec{V}=V_{x}\hat{x} + V_{y}\hat{y} +V_{z}\hat{z}$ which works perfectly! However, in the link you provided, it seems the second equation should be: $$\frac{-V_{x}\cdot\sin(t)+V_{y}\cdot\cos(t)}{r}=f_{\phi}$$ In that case, I get a different plot. What is the reason for that? – David Mar 07 '24 at 19:07