Strange behaviour of $x^2+5x+7$ under iteration

Question

If any of the following exposition is unclear, please write a comment.

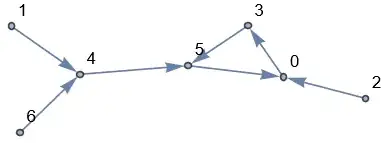
In essence, I am looking at the graph $G$ that is generated by the polynomial $q(x) = x^2+ax+b$ ($a,b \in \mathbb{Z}$) via the edge set $$\{(n, q(n) \text{ mod } p) : n =0,\ldots,p-1\}$$ for some prime $p \in \mathbb{P}$. After some thought, it should be clear that the statements $$``\text{Iterating } q \text{ for any input will always eventually lead to divisibility by some prime at least once.} ``$$ and $$``G \text{ has a path from any node to 0.}``$$ are equivalent. Furthermore, "at least once" can be replaced by "periodically infinitely many times" and "every node has a path to $0$" can be characterized by "$G$ is weakly connected and has exactly one loop containing $0$". With that out of the way, let's get to the question:

The natural question now is to know for which polynomials $q$ we have this nice property of "eventual divisibility" by some prime no matter what number we input, i.e. finding connected $G$ with a single loop containing $0$. This is not rare, see for example $q(x) = x^2+3$ for $p=7$:

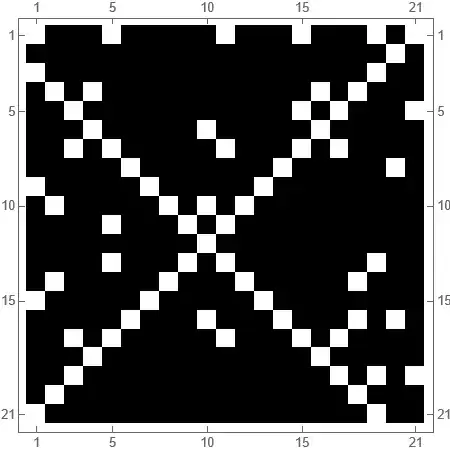
To get a feeling for how rare this is, let's look at the following plot:

This image displays, for $a = -10, \ldots, 10$ on the vertical axis and $b = -10, \ldots, 10$ on the horizontal axis, if $G$ has the aforementioned property for some $p < 113$ in black and otherwise white. There are some obvious cases like $a = b+2$ and $a = -b$ where this eventual divisibility will never occur since they have the one-cycles $(-1,-1)$ and $(1,1)$ respectively.

Modulo careful checking, we can eliminate quite a lot more trivial cases (i.e. explain white squares) in the diagram by searching for trivial one- and two-cycles, i.e. eventual divisibility seems to be the norm rather than the exception. In some other cases, eventual divisibility is found with a somewhat higher prime, such as $p=719$ for $x^2+5x+9$. Sparing you the details, we are left with the cases below, in which either eventual divisibility does not exist or it requires an especially large prime. The discriminant $\Delta$ is included if it helps:

• $x^2-10x-10$ (EDIT) is "eventually divisible" for every residue with $p = 11701$
• $x^2-10x-6$ (EDIT) is "eventually divisible" for every residue with $p = 31237$
• $x^2-10x+4$ (EDIT) is "eventually divisible" for every residue with $p = 6337$
• $x^2-10x+8$ (EDIT) is "eventually divisible" for every residue with $p = 13037$
• $x^2-7x-7$ checked for $p \leq 35800000$ by Mike Daas and me ($\Delta = 77$)
• $x^2-7x+5$ checked for $p \leq 7100000$ by Mike Daas ($\Delta = 29$)
• $x^2+5x+7$ is provably never "eventually divisible" as shown by Oscar Lanzi
• $x^2+3x+7$ (EDIT) is "eventually divisible" for every residue with $p = 225349$

Six of the eight cases above have been solved as indicated, but for the remaining two I cannot rule in or rule out this property. I know that this is a question about (pretty much hopelessly) chaotic behaviour, but perchance somebody has a thought or two on the following:

Since eventual divisibility seems to be occuring by pure chance every time, why do these exceptions stick out so much? Is there some anti-"strong law of small numbers" at work here? If so, are the heuristics that might suggest non-existence of such $G$ for given $q$?

Answer 1

We will never achieve eventual divisibility with $x^2+5x+7$. Cases $p=2$ and $p=3$ fail easily, so we must accept $p>3$ and then reckon with the cases below.

Suppose $p=3k+1$. Then we will have an "isolated" nonzero residue if any such residue solves $x^2+5x+7\equiv x$, thus $x^2+4x+7\equiv 0$. But $x^2+4x+7$ has discriminant $-12$ which is a quadratic residue $\bmod p=3k+1$. So isolated nonzero residues always exist. (The case $p=7$ does give a zero root, but the other root is nonzero.)

Suppose $3k-1$ instead. This time we cannot identify isolated residues, but then $x^2+5x+7$ has discriminant $-3$ which is not a quadratic residue $\bmod p=3k-1$. We can of course try zero residue as an initial condition but would never be able to regenerate it.

The case $x^2+5x+7$ is not unique; a similar result is obtainable whenever we specify $x^2+ax+b$ with $(a-1)^2-4b$ a rational square times $a^2-4b$ and $p=2$ fails. The reader is invited to test this using $x^2+17x+75$.

---

A second approach, which works on some other quadratic function iterations, involves using discriminants to show a contradiction between eventual divisibility and the existence of 2-cycles. Given a quadratic iteration function $x^2+ax+b$, the roots for primitive 2-cycles (not those where a single invariant residue is simply repeated twice) is

$x^2+(a+1)x+(a+b+1)\equiv0.$

If $a$ and $b$ have a right parity combination to avoid eventual divisibility with $p=2$, then a proof similar to the one above may be set up whenever the discriminant for the above equation is a rational square times the $a^2-4b$ discrimiant from the iteration function. However, we still must explicitly test prime factors of the constant term $a+b+1$ for which residue $0$ is part of the 2-cycle. An example is provided by the iteration of $x^2-9x+19$ for which the primitive 2-cycle equation becomes $x^2-8x+11\equiv0$. These have discriminants $5$ and $20=4×5$ respectively, so we either have a 2-cycle if $p$ is a quadratic residue $\bmod 5$ or no chance for a zero residue if $p$ is a nonquadratic residue (the double root at $p=5$ is nonzero and thus of no consequence). But we must still test $p=11$ explicitly because residue $0$ appears in the 2-cycle. In this example nondivisibility holds with other residues $\bmod11$, but a similar analysis with $x^2+3x+3$ reveals that eventual divisibility slips through for (only) $p=7$.

Answer 2

Oscar Lanzi has already given quite a nice overview over a general method to attack a certain set of polynomials trying to disprove eventual divisibility. Let's explore this idea a bit further and give a nice summary of the method:

We start with defining $q(x) := x^2+ax+b$ and examine solutions to $q(x) = x$ and $q(x) = 0$ to set up the method. For $p \neq 2$, we can derive the quadratic formula over $\mathbb{F}_p$ in exactly the same way as over $\mathbb{R}$ (using modular inverses) and obtain $$x^2 + cx + d \text{ is solvable in $\mathbb{F}_p$} \iff \Delta = 4^{-1}c^2 - d \text{ is a quadratic residue in $\mathbb{F}_p$}$$ For $p = 2$, the usual method breaks since we would have to divide by $2 \equiv 0 \mod 2$. This can be accounted for by checking the parities of the coefficients seperately. To now arrive at a contradiction, we need to have:

• $q(x) = x$ solvable and $q(x) = 0$ not solvable for any $p \in \mathbb{P}$

Why? Because this guarantees that there is fixed point of $p$ that is not zero, since then $q(0) = 0$ would need to be true -- contradicting the second property. As mentioned in the question, this is a sufficient crition to ensure non-eventual divisibility. To actually use the $\Delta$-property to find such $q$, we need to cover all primes using properties of quadratic residues.

Quadratic reciprocity and the chinese remainder theorem tell us that covering all the primes in this fashion is only possible if the discriminants have the same prime factors up to squared factors, i.e. $\Delta(q(x)-x) = m^2 \Delta(q(x))$ for some $m \in \mathbb{Q}$ where $\Delta$ is the discriminant of the polynomials in the argument. This exact same method can also be applied to $q(q(x)) = x$ instead of $q(x) = x$ and higher iterates to obtain different sets of solutions. Be careful: For higher iterates we still need to check if $q(...q(x)) = 0$ for some lower amount of iterates along the way, since $0$ could be part of this cycle. Since all residues inside a cycle must be solutions to the ($n$-times) iterated fix-point equation, we know that zero will be part of the cycle if $$q^{(k)}(0) = 0 \mod p \text{ for some } k | n$$ i.e. if $q$ is not eventually divisible for every prime factor $p$ of the constant term (of iteration numbers dividing $n$), we have disproven eventual divisibility. Taking only the "true" factors of the iterates $q^{(n)}(x)-x$ not contained in lower order iterates, we need to check the divisibility of the following constant terms for each cycle length: $$\begin{matrix} n=1: 2 \text{only} \\----\\ n=2: [a+b+1] \\----\\ n=3: [b^3+(2+2a)b^2+(1+3a+a^2)b+a^2+a+1] \\----\\ n=4: [b^6+(3+3a)b^5+(3a^2+8a+3)b^4+(a^3+7a^2+7a+3)b^3+(2a^3+5a^2+5a^2+2)b^2+(a^3+2a^2+3a)b+a^2+1] \end{matrix}$$

(For $n=1$, there will always be a nonzero isolated residue unless $a=1$; but then $a=1, b$ odd does not allow any cases where the two discriminants are rational squares times each other.) In all cases, if $\Delta$ for the original quadratic function $x^2+a+b$ contains any prime factors not present in the discriminant of $q^{(n)}(x)-x$ then those factors should also be tested. This is about the most you can get out of this method besides brute-force.

Let's compute a couple of cases that fulfill these conditions and the parity condition $a \equiv b \mod 2$ for tuples $(a,b)$ with $|a|,|b| \leq 100$:

• $q(x) = x$ solvable and $q(x) = 0$ not solvable with $\Delta(q(x)-x) = m^2 \Delta(q(x))$: $$\require{enclose} (-19,87), \enclose{horizontalstrike}{(-17,61)} \text{ [$p$ = 3]}, (-16,60), \enclose{horizontalstrike}{(-13,61)} \text{ [$p$ = 5]}, (-10,24), (-10,32), (-7,19), (5,7), (8,12), (11,37), \enclose{horizontalstrike}{(13,31)} \text{ [$p$ = 3]}, (14,40), (17,75), \enclose{horizontalstrike}{(17,91)} \text{ [$p$ = 5]}, (18,72), (18,88), (20,84)$$
• $q(q(x)) = x$ solvable and $q(x) = 0$ not solvable with $\Delta(q(q(x))-x) = m^2 \Delta(q(x))$: $$\require{enclose}(-14,44), (-7,11), (-6,12), (6,4), (11,29), \enclose{horizontalstrike}{(13,31)} \text{ [$p$ = 3]}, (16,44)$$
• $q(q(q(x))) = x$ solvable and $q(x) = 0$ not solvable with $\Delta(q(q(q(x)))-x) = m^2 \Delta(q(x))$: $$(-21,-41), (-17,25), (-17,71), (-14,56), \enclose{horizontalstrike}{(-2,0)} \text{ [$p$ = 3]}, (3,-9), \enclose{horizontalstrike}{(4,0)} \text{ [$p$ = 3]}, (14,40), (19,7), (19,89)$$
• $q(q(q(q(x)))) = x$ solvable and $q(x) = 0$ not solvable with $\Delta(q(q(q(q(x))))-x) = m^2 \Delta(q(x))$: $$(15,53)$$