3

Nice feature I just came up with

We have two conic sections, and we draw the common tangents to the two conic sections. The points of contact on the two conic sections lie on one conic section.

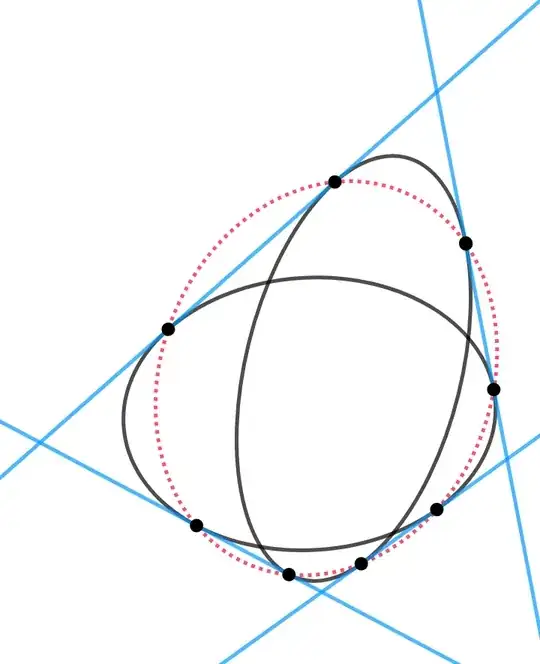
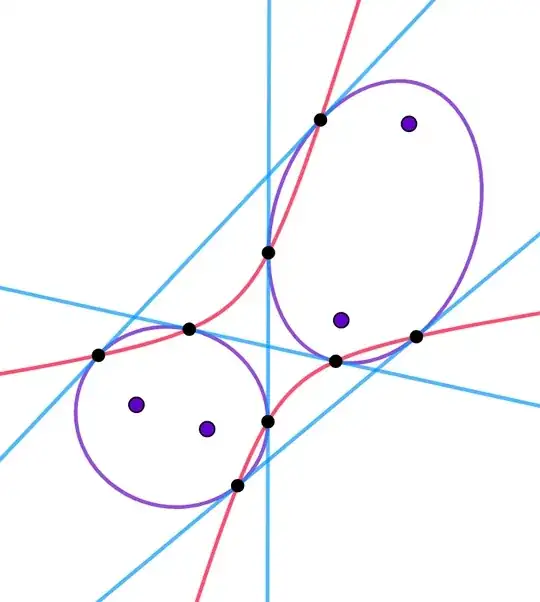
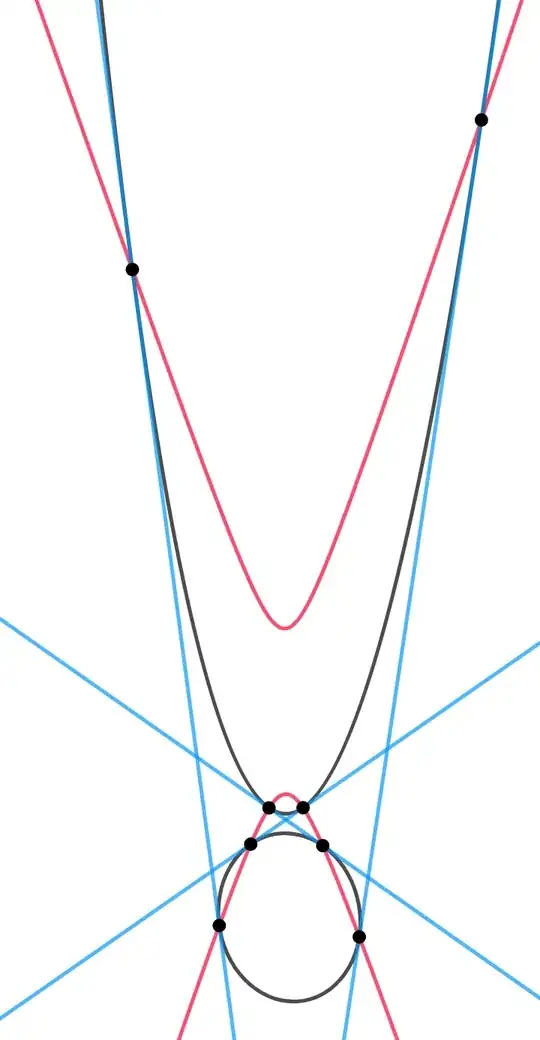
enter image description here

enter image description here

enter image description here

Is this feature already known?

How do we prove that anyway?

brainjam
  • 9,172
زكريا حسناوي
  • 4,060
  • 7
  • 25
  • 2
    This conic is known under the name "Eight-points conic" – Jean Marie Jan 20 '24 at 18:15
  • Thank you Jean Marie, it is expected to be already discovered because it is a preliminary feature, that's okay, I will look for other features, and share more features that I come up with over time – زكريا حسناوي Jan 21 '24 at 04:50
  • 1
    @JeanMarie: Is this really the Eight-Points Conic? The note you cite defines 8PC as passing through the two given conics' four points on intersection and four more pointa at the intersections of four associated tangent lines (two per conic). OP's conic doesn't even require the given conics to meet, and the tangent lines involved each touch both given conics. – Blue Jan 21 '24 at 09:36
  • 1
    @Blue You are right : It's not in fact the same conic ! – Jean Marie Jan 21 '24 at 12:26
  • Thank you, Blue. I was in a hurry and did not notice that it was a different conic section. Indeed, it is different, and there is still hope that this beautiful property is new and previously unknown. – زكريا حسناوي Jan 21 '24 at 13:19

1 Answers1

1

This conic (I'll call it $F$) is discussed in the classical projective geometry literature. I've seen it variously referred to as "Salmon's conic", "covariant conic" and "harmonic locus". It has the remarkable property that, for any point $P$ on $F$, the four tangents from $P$ to the two original conics form a harmonic set, i.e. their cross ratio is $-1$.

For a synthetic treatment, see Hatton, Projective Geometry, pg. 293, Article 133.

For an analytical treatment, see Salmon, Conic Sections, pg 306, Article 334 (see also Article 378, pg 344).

The above references also discuss the dual curve. I've seen applications of $F$ to topics such as conics in double contact, and Poncelet's porism.

brainjam
  • 9,172