1

Consider the Bregman divergence induced by negative entropy function $$ D_h(x||y) = -\sum x_i + \sum y_i +\sum x_i\ln \frac{x_i}{y_i} $$

Given a constrained simplex $K_\alpha = [x\in [\alpha,1]^d | \sum x_i = 1]$ with $\alpha\in [0,1/d]$. What is the Bregman projection of a non-negative vector $y$ to $K_\alpha$? In other words, given $y\in R_+^d$, what is $y^+$ defined as $$ y^+ = \arg \min_{x\in K_\alpha} D_h(x||y) $$ ?

It's known that when $\alpha=0$, $y^+ = \frac{y}{||y||_1}$. I am wondering if there is a closed form for $y^+$ for general $\alpha$.

Thanks in advance!

Royi
  • 10,050
Vassily
  • 451
  • 3
  • 10
  • Have you tried duality, like the standard approach of projecting onto the unit simplex via the Euclidean norm? Give one Lagrange multiplier to the equality constraint. Get a concave dual in one variable. Solve by bysection --> use the primal-dal relationship to solve the primal. – Alex Shtoff Dec 28 '23 at 09:05
  • @Royi it is convex, since $K_\alpha$ is a convex set. It's the intersection of the box $[\alpha, 1]^d$ with the hyperplane defined by $\sum_{i=1}^n x_i=1$. – Alex Shtoff Dec 10 '24 at 14:03

1 Answers1

0

I will solve the problem using an iterative method.

In 2D the constraint set for $\alpha = 0.4$ is given by:

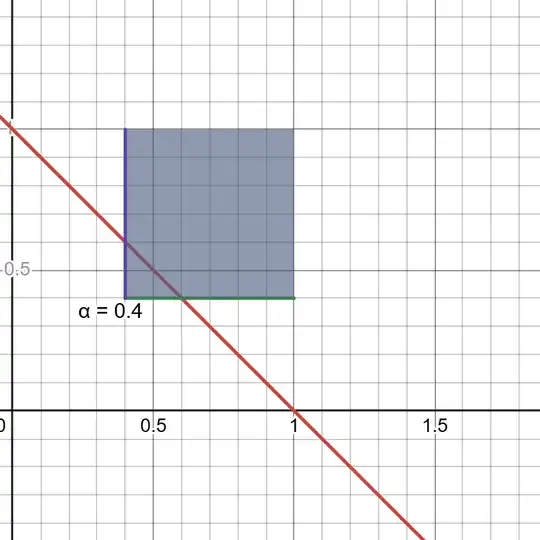
enter image description here

It is a convex set as @AlexShtoff pointed out.

One easy way to solve the problem is the Projected Gradient Descent.
One need two components to solve this:

  1. The Gradient
  2. The Projection onto the Constraints Set

The Gradient

The function is given by:

$$ f \left( \boldsymbol{x} \right) = -\boldsymbol{1}^{T} \boldsymbol{x} + \boldsymbol{1}^{T} \boldsymbol{y} - \boldsymbol{1}^{T} \left( \boldsymbol{x} \odot \ln \left( \boldsymbol{x} \right) - \boldsymbol{x} \odot \ln \left( \boldsymbol{y} \right) \right) $$

Hence the gradient is given by:

$$ \nabla f \left( \boldsymbol{x} \right) = \ln \left( \boldsymbol{x} \right) - \ln \left( \boldsymbol{y} \right) $$

Projection onto Unit Simples with Minimum Boundary Constraint

Similar to Orthogonal Projection onto the Unit Simplex.
With the difference being the function to find its root is given by:

$$ h \left( \mu \right) = \sum_{i = 1}^{n} { \left( {y}_{i} - \mu \right) }_{+\alpha} - 1 $$

Where ${ \left( x \right) }_{+\alpha} = \max \left\{ x, \alpha \right\}$.

Since $h \left( \cdot \right)$ is a piece wise linear function it should be evaluated at its joints which are given by ${y}_{i} - \mu = \alpha$.
Hence the evaluation points are ${y}_{i} - \alpha$.
Then the rest is as the case of $\alpha = 0$ as linked.

This is a 2D solution:

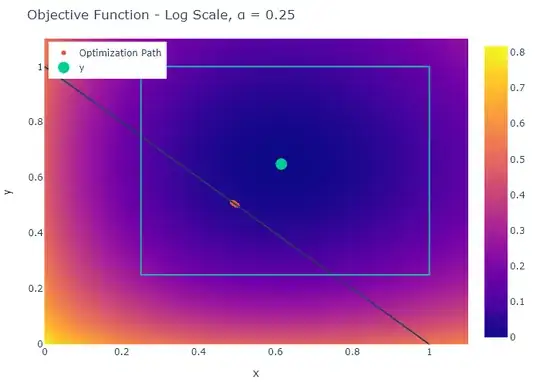
enter image description here

The code is available on my StackExchange Mathematics GitHub Repository (Look at the Mathematics\Q4834628 folder).

Royi
  • 10,050