True or false: For every $n\in\mathbb{Z^+}$, there exist $a,b,c$ such that $y=(x-a)^2+b$ and $y=c$ enclose exactly $n$ lattice points.

Question

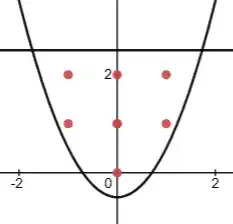
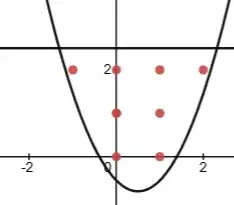
It is easy to show that, for every $n\in\mathbb{Z^+}$, there exists a circle that encloses exactly $n$ lattice points (points with integer coordinates). Can we say the same thing about a parabola and a horizontal "cap" at the top?

True or false: For every $n\in\mathbb{Z^+}$, there exist $a,b,c$ such that $y=(x-a)^2+b$ and $y=c$ enclose exactly $n$ lattice points. If a point lies on the curve or the horizontal line, then the point is considered to be enclosed.

For example, $y=(x-0)^2-0.5$ and $y=2.5$ enclose exactly $7$ lattice points.

$y=(x-0.5)^2-0.8$ and $y=2.5$ enclose exactly $8$ lattice points.

But as $n$ gets larger, more fine tuning is needed to enclose exactly one more lattice point than before, and I don't know if it will always be possible to do so.

Context: I was trying to draw a parabola using basic equipment, and this conjecture came to mind.

Answer 1

A similar argument to the answer in the linked question works here. Let

$$(a,b,c)=(\pi,b,1/2)$$

Decreasing $b$ will lower the parabola, adding more and more points. Note that no points are ever added on the top line as $c$ is not integral. Can two lattice points ever be added at the same time? No, since then

$$k_1=b+(n_1-\pi)^2$$

$$k_2=b+(n_2-\pi)^2$$

for some integer pairs $(n_1,k_1)$ and $(n_2,k_2)$. Also note that $n_1\neq n_2$. This implies

$$k_1-(n_1-\pi)^2=k_2-(n_2-\pi)^2$$

$$\Rightarrow \pi=\frac{k_1 - k_2 + n_2^2 - n_1^2}{2 (n_2- n_1)}$$

which is impossible since $\pi$ is irrational.