How to draw a parabola using basic equipment?

Question

A straight line can be drawn with a straightedge.
A circle can be drawn with a compass.
An ellipse can be drawn with string and pins.

How can we draw a parabola, using basic equipment?

Remarks

The parabola should be "perfect" (like a circle drawn with a compass), not just a rough sketch. As far as how much of the parabola should be shown: enough so that it looks like a "U".

We can use basic equipment such as string, pins, etc. The simpler the equipment, the better (so for example, a method using an unmarked straightedge is better than a method using a marked straightedge). High tech tools like computers are not allowed. You are given paper, pen and a flat table.

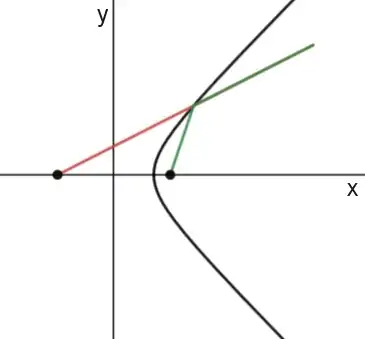
We can define a parabola as the set of points in a plane equidistant to a fixed line (directrix) and a fixed point (focus), or use any equivalent definition.

I tried to find how the ancient Greeks physically drew parabolas, but found nothing.

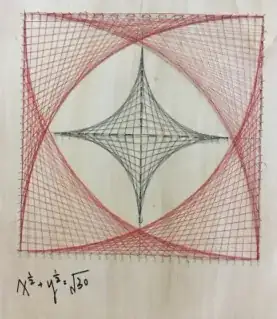
Students at my school made an almost-perfect parabola using strings and pins, by setting strings such that for each string the sum of its $x$- and $y$- intercepts is $30$, so the strings are tangent to an envelope curve $\sqrt x + \sqrt y = \sqrt{30}$, which is a rotated parabola.

But this is not quite what I'm looking for, because it's not quite perfect, as the number of strings is finite.

In this video a carpenter shows how to make a beautiful almost-perfect parabola, similar to the string art above, but again it's not quite perfect because the number of lines is finite.

If it's not possible to draw a perfect parabola using basic equipment, then is there an explanation?

Answer 1

Here is video of a brilliant "conic section compass".

Here is a closer look at how it works. It is very simple: the axis of the compass is the axis of a cone. The pencil is a slanting "edge" of the cone. The axis of the cone, and the axis of the pencil, intersect at the vertex of the cone. The paper is a plane intersecting the cone. The pencil traces the intersection of the plane and the cone - literally, a conic section.

Answer 2

From the comments, @Intelligentipauca found A Geometrical Treatise on Conic Sections. Page 4 shows:

This is exactly what I was looking for.

Extension to hyperbola

This approach could also be used to draw a hyperbola.

The bar is shown in red, the string is shown in green (the string covers part of the bar). Note that the bar is longer than the string by a certain length. The bar and string are connected on the right.

The left end of the bar pivots around the left focus point. The other end of the string is attached to the right focus point.

The pen is fixed to a sliding point on the bar. As the bar pivots, the string is kept taut by the pen (a rubber band connecting the left left focus point and the tip of the pen would do the trick).

As the bar pivots, the pen traces a hyperbola. As the bar pivots, the gradient of the bar approaches the gradient of the asymptote of the hyperbola. (To draw more of the hyperbola, get a longer bar and string.)

Ancient Greeks

After I posted my question, I found that, according to the bottom of page 2 of a book on conic sections, the ancient Greeks "were not able to construct conics in the plane". I guess they would not have fancied the method of construction described above.

Answer 3

This can be done if your "basic equipment" includes a contraption that allows a triple of concurrent lines (say, rods) to slide freely while retaining the concurrence. The key mathematical tool is Pascal's theorem, or more precisely its converse, known as https://en.wikipedia.org/wiki/Braikenridge%E2%80%93Maclaurin_theorem.

The Braikenridge-Maclaurin theorem may be applied in the Braikenridge-Maclaurin construction, which is a synthetic construction of the conic defined by five points, by varying the sixth point. Namely, Pascal's theorem states that given six points on a conic (the vertices of a hexagon), the lines defined by opposite sides intersect in three collinear points. This can be reversed to construct the possible locations for a sixth point, given five existing ones.

This result allows one to construct, using a ruler only, an arbitrary point on a conic section passing through given 5 points. If one chooses the five points so that the resulting conic will be a parabola, this gives a way of constructing a parabola, in the following sense: given an arbitrary line $\ell$ through A, one constructs the point on $x$ which lies on the conic.

Thus, if one starts for example with the five points $(0,0)$, $(1,1)$, $(-1,1)$, $(2,4)$, $(-2, 4)$, one will obtain as output the standard parabola $y=x^2$.

There is a nice animation here for the case of the parabola: https://en.wikipedia.org/wiki/Five_points_determine_a_conic#Construction

Answer 4

You can define the parabola as an envelope of lines. Start with the focus $F$ and directrix line $l$. Select points $P_k$ on $l$ and construct the perpendicular bisector $m_k$ between $F$ and each $P_k$.

At any point on $m_k$ for each $k$, the distance to $F$ is equal to the distance to $P_k$. But the distance from a point on $m_k$ to $l$ as a whole is less except at one point where $m_k$ meets the perpendicukar to $l$ from $P_k$. Thus $m_k$ is tangent to the parabola for all $k$ and the parabola is defind as the envelope of all tge perpendicular bisectors.

As with other envelope curves, you can realize this definition with good accuracy by constructing perpendicular bisectors to a sufficiently close-packed set of directrix points $P_k$.