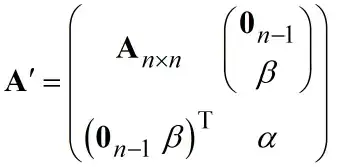I have a real $n \times n$ symmetric matrix $\mathbf{A}_{n \times n}$ which I would like to extend with a row/column pair:
where $\alpha$ and $\beta$ are two real numbers and $\mathbf{0}_n$ is a zero vector of size $n$.
Is there any effective algorithm which is able to compute the eigenpairs of $\mathbf{A}'$, using the eigenpairs of $\mathbf{A}_{n \times n}$?