How to Flip a Bell Curve Upside Down?

Question

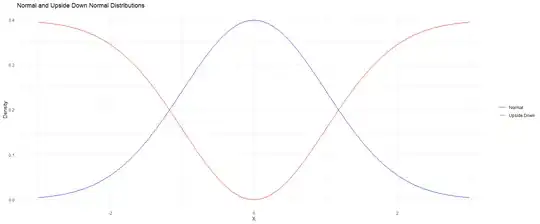
I am interested in learning about if its possible to make an upside down bell curve (i.e. upside down normal distribution) such that the final result is a valid probability distribution function.

That is, the "peak" now has the lowest probability and the tails now have the highest probabilities ... and the integral of this new distribution still integrates to 1.

Using computer programming languages (e.g. R), I know this is possible. For example:

library(ggplot2)
x <- seq(-3, 3, by = 0.01)
y <- dnorm(x)
y_upside_down <- max(y) - y
df <- data.frame(x = c(x, x), y = c(y, y_upside_down), curve = rep(c("Normal", "Upside Down"), each = length(x)))
ggplot(df, aes(x = x, y = y, color = curve)) +
    geom_line() +
    scale_color_manual(values = c("Normal" = "blue", "Upside Down" = "red")) +
    theme_minimal() +
    labs(x = "X", y = "Density", title = "Normal and Upside Down Normal Distributions") +
    theme(legend.title = element_blank())

But now I am wondering, what would the corresponding function look like for the red curve?

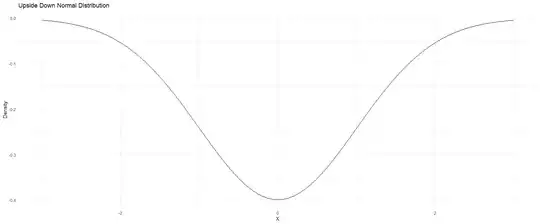
Idea 1: The first thing that came to mind was just to take the negative of a normal distribution :

$$-f(x) = \frac{1}{\sqrt{2\pi}} e^{-\frac{(x-\mu)^2}{2}}$$

But this will have negative densities, and this is not possible (i.e. not a valid probability distribution):

x <- seq(-3, 3, by = 0.01)
y_upside_down <- -y
ggplot(data.frame(x = x, y = y_upside_down), aes(x = x, y = y_upside_down)) +
    geom_line() +
    theme_minimal() +
    labs(x = "X", y = "Density", title = "Upside Down Normal Distribution")

Idea 2: The other idea I had was to take this negative function and shift it vertically by the maximum point - but likely also won't result in a valid probability distribution (i.e. will not integrate to 1):

$$f_{\text{mirrored}}(x) = f_{\text{max}} - f(x)$$

Can someone please show me how to do this correctly? Is there an exact probability distribution that corresponds to the upside down normal distribution? Or is there some method I can use to transform the regular normal distribution into the distribution I am looking for?

Thanks!

References:

• Upside down bell shaped graph moving with respect to $x$ axis

Answer 1

An upside down bell-curve can never give you a valid probability distribution function. This is because for any valid pdf $f_X(x)$, we must satisfy the condition $\displaystyle \int_{-\infty}^\infty f_X(x)dx = 1$. Note that this means that the integral of the pdf over the real line is finite. This could happen when:

1. The negative part of the function cancels out with part of the positive part of the function, eg. with the function $\operatorname{sinc} x$. In this case it is not possible, as a valid pdf must always have $f_X(x) \geq 0$.
2. The function is wholly positive and tends to $0$ as $x$ tends to $\infty$ or $-\infty$. In the case of the inverted bell curve, the function would constantly be increasing as $x$ tends to both $\infty$ or $-\infty$, tending towards some fixed positive value, $k$, without ever reaching it. Thus the value $\displaystyle \int_{-\infty}^\infty f_X(x)dx $ MUST diverge.