Recursive functional $\sqrt{2^x}$

Question

I'm looking to study a function $φ$ that verifies $(φ \circ φ)(x) = \sqrt{2^x}$.

My approach is as follows: try to express $φ$ in the form of a limited expansion.

Posing $φ(x) = a_0 + a_1x + a_2x^2 + ... + a_nx^n$.

I then replace $x$ by $φ(x)$ to obtain the development of $φ \circ φ$.

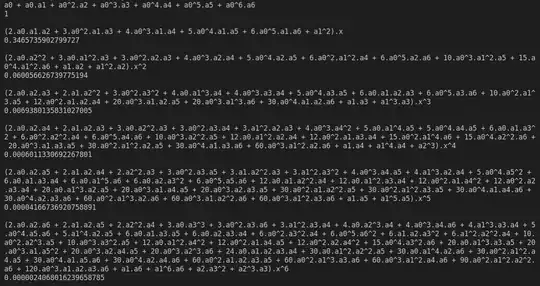
I thus obtain a system of equations because the coefficients must correspond to those of $\sqrt{2^x}$.

Here are the first equations with a 6th-order approximation.

Unfortunately , the task seems difficult , which makes me I wonder if this approach is right ...

Would you have alternative approaches & any references on this subject that I might find pertinent ?

Thanks in advance!

I dislike ${√2}^x$ even though $(\sqrt 2)^x =\sqrt{(2^x)}$ — Henry, Nov 09 '23 at 12:02
Make it simpler writing instead $e^{b x}$ and use less terms. This would be a nightmare. — Claude Leibovici, Nov 09 '23 at 12:17

score 0 · Accepted Answer · answered Nov 09 '23 at 14:17

[[ Difficult to get through with this !
I am Posting this longish Comment to aid OP. ]]

We should have a way to get $y_1(y_1(x))=e^x$

We will then have to tweak that to get $y_2(y_2(x))=e^{ax}$

We can then let $a=\log(2)/2$

That will give this : $y_3(y_3(x))=e^{x\log(2)/2}=\sqrt{e^{\log(2)}}^x=\sqrt{2}^x$

Eventually , the closed-form function might not [ will not ?? ] exist & other ways to express the function might be very cumbersome & tough to make.

Check out :

1 Answers1