Let us rewrite. We are searching the minimal value of the expression
$$
P(a,b,c)=
\frac
{\sqrt{a+1} + \sqrt{b+1} + \sqrt{c+1}}
{\sqrt{(a+1)(b+1)(c+1)+1}}
$$
constrained to the relation $a+b+c+abc=4$.
It turns out it is $\sqrt K$,
$$
P(a,b,c)\ge \sqrt K\ ,\qquad K=\frac1{10}(1+2\sqrt 3)^2=\frac 1{10}(13+2\sqrt 7)\approx 1.9928203230275\dots\ \ .
$$
Let us show this.
It is convenient to substitute $x,y,z\ge 1$ for $\sqrt{a+1}$, $\sqrt{b+1}$, $\sqrt{c+1}$.
And let us use the symmetric elementary functions $p,q,r$ for the variables $x,y,z$, so $p=x+y+z$, $q=xy+yz+zx$, $r=xyz$.
The relation satisfied by $x,y,z$ is:
$$
x^2y^2z^2 -x^2y^2 -y^2z^2-z^2x^2 +2x^2+2y^2+2z^2-8=0\ .
$$
In terms of $p,q,r$ it is:
$$
r^2 -(q^2-2pr)+2(p^2-2q)-8=0\ .
$$
So we solve a related problem first, we minimize the following function
$F$ on the domain $p\ge 3$, $q\ge 3$, $r\ge 1$, $p^2\ge 3p$ (which is $\sum(x-y)^2\ge 0$ with equality iff $x=y=z$), and $p(p^2-3q) + 6r\ge pq-3r$ (which is $x^3+y^3+z^3+3xyz\ge x^2(y+z)+y^2(z+x)+z^3(x+y)$, Schur). Note that the Schur inequality becomes an equality if and only if two involved variables are equal, this is also the case we obtain equality in $P\ge \sqrt K$. We restate this as $P^2\ge K$, and further as $(x+y+z)^2\ge K(x^2y^2z^2+1)$. So we consider the minimization of $F$,
$$
F(p,q,r):=p^2-K(r^2+1)\ ,
\qquad\text{ constrained to }
\underbrace{r^2-(q^2-2pr)+2(p^2-2q)-8}_{h(p,q,r)}=0\ .
$$
Lagrange multiplicators. In case of a local extremal value in the domain (two-dimensional) $h(p,q,r)=0$, with boundaries given by the above boundary conditions, the coresponding extremal point satisfies $0=G'_p=G'_q=G'_r=G'_m$ for
$$
G(p,q,r;m):=
F(p,q,r)-mh(p,q,r)\ .
$$
The corresponding system is:
$$
\left\{
\begin{aligned}
0&=2p-m(2r+4p)\ ,\\
0&=-m(-2q-4)\ ,\\
0&=-2Kr-m(2r+2p)\ ,\\
0&=h(p,q,r)\ .
\end{aligned}
\right.
$$
The condition $0=G'_q$ makes everything clear. ($F$ does not depend on $q$.) The factor $2q+4$ does not vanish in the given region. Also, $m=0$ leads to $p=r=0$, again outside of the sight. So any extremal value for $F$ constrained to $h=0$ is a boundary point.
Each of the boundary conditions $p=3$ and/or $q=3$ and/or $r=1$ and/or $p^2=3q$ leads to $x=y=z$ thus to $a=b=c$, and the common value is $1$ from the given $(a,b,c)$-condition. In this case $x=y=z=\sqrt 2$, $p=3\sqrt 2$, $r=2\sqrt 2$, and
$$
\begin{aligned}
F(3\sqrt 2,*,2\sqrt 2)
&=(3\sqrt 2)^2-K((2\sqrt2)^2+1)=18-9K=9(2-K)
\\
&=
\frac 9{10} (7-4\sqrt 3)
=\frac 9{10} \cdot \frac {49-48}{7+4\sqrt 3}
>0\ .e
\end{aligned}
$$
It remains to check the remained boundary condition, the Schur condition on $p,q,r$, taken with equality. This happens iff two values among $x,y,z$ (equivalently among $a,b,c$) are equal. Here, we can go back to $P$, assume $a=c$, write $b$ in terms of $a$ as $b=b(a)=2(2-a)/(a^2+1)$, so $a\in[0,2]$, and minimize the ugly function in one variable
$$a\to g(a)=\Bigg( \ 2\sqrt{a+1} +\sqrt{b(a)+1}\ \Bigg)^2-K\Bigg(\ 1 + (a+1)\sqrt{b(a)+1} \ \Bigg)\ , \qquad g:[0,2]\to\Bbb R\ .
$$
In a plot:
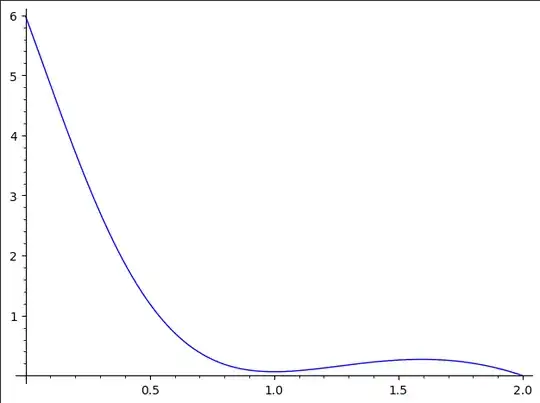
I hope, everybody who considered the problem will find from here her or his way to proceed.
Humanly, the problem starts now, i have no chance to finish in time as a human. The reason is the following one. We have a more or less complicated function. Its study must somehow involve analytic tools like taking derivatives, consider critical points, compute the value in these points. Then also compute the values at the ends of the interval $[0,2]$, and finally decide which candidate wins the minimum prize.
Well, this consideration must then find the critical point $a=1$, which is easy to check in any system of equations, but also that local max between $1$ and $ 2$. And this point is no longer "easy".
So let us work algebraically with the aid of a computer.
We are searching for globally minimal points $(a,b,c)$ for $P$ with $a=c$.
Let us pass to the $(x,y,z)$ coordinates via $a=x^2-1$, $b=y^2-1$, the condition $a=c$ becomes $x=z$, so we want to minimize
$$
\begin{aligned}
F(x,y ) &= (2x+y)^2-K(x^4y^2+1)\ ,\\
&\qquad\text{ constrained to }
\\
0 &= \underbrace{2(x^2-1)+(y^2-1)+(x^2-1)^2(y^2-1)-4}_{h(x,y)}\ .
\end{aligned}
$$
We have two new functions $F,h$. Lagrange multiplicators for them.
We obtain an ugly algebraic system of high degree. Let us ask the
machine for solutions with $x,y\ge 1$.
L.<w> = QuadraticField(3)
K = (1 + 2*w)^2/10
R.<x, y, m> = PolynomialRing(L)
F = (2x + y)^2 - K(x^4y^2 + 1)
h = 2(x^2 - 1) + (y^2 - 1) + (x^2 - 1)^2*(y^2 - 1) - 4
J = R.ideal([diff(F - m*h, v) for v in (x, y, m)])
variety = J.variety(ring=AA)
for dic in variety:
x0, y0, m0 = dic[x], dic[y], dic[m]
if not(x0 >= 1 and y0 >= 1):
continue
a0, b0 = x0^2 - 1, y0^2 -1
print(f"Critical point with components:")
print(f"(x, y) = ({x0}, {y0})")
print(f"(a, b) = ({a0}, {b0})")
print(f" F-value = {F.subs(x=x0, y=y0)}")
And we obtain:
Critical point with components:
(x, y) = (1.414213562373095?, 1.414213562373095?)
(a, b) = (1, 1)
F-value = 0.06461709275204174?
Critical point with components:
(x, y) = (1.610339275596270?, 1.109030006353267?)
(a, b) = (1.593192582527918?, 0.2299475549919257?)
F-value = 0.2710105546461977?
This values are now compared with the values at the extremities of the interval, and the value in $(a,b)=(2,0)$, corresponding to $(x,y)=(\sqrt 3,1)$ wins, the function $F$ is zero, the global minimum.

solution = Reduce[constraint, {a, b, c}, Reals]
minimum = NMinimize[{f[a, b, c], solution}, {a, b, c}]`
Mathematica shows (a,b,c)=(2,2,0) or (2,0,2) or (0,2,2) may minimize $P$
– 138 Aspen Nov 03 '23 at 15:02